Учебная работа. Доклад: Вероятность случайного события

Учебная работа. Доклад: Вероятность случайного события

Событие именуется случайным, если в итоге тесты (опыта) оно может произойти, а может и не произойти.

Примеры.

Испытание – бросание монеты, случайное событие – выпадение герба.

Испытание – роль в игре “Российское лото”, случайное событие — выигрыш.

Испытание – прыжок с парашютом, случайное событие – удачное приземление.

Испытание – рождение малыша, случайное событие – пол малыша – мужской.

Испытание – наблюдение за погодой в течение денька, случайное событие – в течение денька был дождик.

Как лицезреем пришествие случайного действия в итоге тесты, совершенно говоря, недозволено предсказать заблаговременно в принципе. Данный факт – непредсказуемость пришествия – можно в неких вариантах считать основным отличительным свойством случайного действия. Тем не наименее, имеется возможность некие случайные действия подвергнуть анализу способами арифметики.

Пусть некое испытание произведено раз и в итоге этого связанное с ним случайное событие (обозначим его через А) вышло раз. Тогда относительной частотой случайного действия А, назовем отношение к . Иными словами . Для почти всех случайных событий относительная частота владеет свойством стойкости, другими словами в разных длинноватых серия испытаний относительные частоты 1-го и такого же случайного действия не много различаются друг от друга. Случайные действия, относительные частоты которых, владеют свойством стойкости, именуются постоянными.

Устойчивость относительной частоты была найдена и неоднократно доказана экспериментально естествоиспытателями в 17-19 веках. Более впечатляющим является итог К. Пирсона, который кидал монету 12000 раз, потом выполнил еще одну серию бросаний – 24000 раз. В этих сериях он подсчитывал количество выпадений герба и получил значения относительной частоты для него 0,5016 и 0,5005, отличающиеся друг от друга на 0,0011.

Для случайных событий владеющих свойством стойкости, относительную частоту пришествия действия естественно считать степенью способности пришествия случайного действия.

Пример. Баскетболист А из некого положения попал в кольцо 4 раза при 11 бросках. Баскетболист В из этого же положения – 6 раз при 18 бросках. Какому из игроков доверить выполнение штрафного удара из этого положения?

Решение. Найдем относительные частоты попадания в кольцо этими игроками:, . Потому что , то выполнение штрафного лучше доверить игроку А. Если относительная частота больше, то больше и уверенность в успехе.

При использовании относительной частоты в качестве меры способности пришествия случайного действия появляются две трудности. 1-ая – в различных сериях испытаний получаются различные значения частоты, неясно какое из приобретенных значений “наиболее поистине”. 2-ая – относительную частоту можно отыскать лишь опосля испытаний, при этом желательна довольно длинноватая серия, потому что свойство стойкости проявляется тем отчетливее, чем длиннее серия. Все это вкупе взятое принуждает находить методы конкретного определения меры способности пришествия случайного действия, при этом до тесты, до опыта.

Сначала определим возможность постоянного случайного действия как число, около которого колеблется относительная частота в длинноватых сериях испытаний. Потом введем понятие равновозможности, равновероятности 2-ух событий. Смысл этого понятия ясен интуитивно, цель введения — мы желаем найти математически понятие вероятности сводя его к наиболее обычному не определяемому понятию равновероятности. наличие равновероятности неких событий являющихся финалами некого тесты устанавливается из “общих суждений”, не доказывается математически и не быть может подтверждено, не нуждается в подтверждении как первичное. к примеру, при бросании игральной кости выпадение 1, 2, … , 6 очков считают событиями равновероятными (либо “практически” равновероятными) исходя из предполагаемой физической однородности материала кости и геометрической корректности, другими словами считая кость безупречным кубом. Если в итоге тесты может быть пришествие равновозможных событий, никакие два из которых не могут наступить сразу, то возможность всякого из этих событий определяется как , а сами действия именуются простыми событиями либо простыми финалами.

Если, событие А инициируется одним из простых исходов, а самих исходов по прежнему , то возможность действия А обозначаемая как , определяется как отношение к . По другому: . (Формула традиционной вероятности)

Пример. Обозначим – выпадение 1, …, 6 очков при бросании игральной кости. . Пусть А – выпадение четного числа очков, тогда и .

тут уместно привести комментарий соответствующий для физики: относительные частоты постоянных случайных событий, приобретенные в длинноватых серия испытаний, отлично согласуются со значениями отысканными по формуле традиционной вероятности.

Примеры решения задач.

А) Студент, готовясь к экзамену, успел приготовить 18 билетов из 25. Какова возможность вытащить на экзамене “неплохой” билет?

Решение.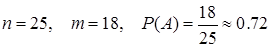

Б) Какова возможность, что при бросании 2-ух игральных кубиков сумма выпавших очков меньше 5?

Решение. Всего два кубика могут выпасть 36 методами: (1;1), (1;2), …(1;6), (2;1), (2;2), …, (2;6), (3;1), …, (6;6). Все эти финалы считаем равновозможными, не наступающими сразу, означает . Обозначим через А событие: при бросании 2-ух игральных костей, сумма выпавших очков меньше 5. Событие А определяется финалами (1;1), (1;2), (2;1), (1;3), (3;1), (2;2), другими словами . По формуле традиционной вероятности получаем .

В) Лифт в пятиэтажном доме отчаливает с 3-мя пассажирами с первого этажа. Отыскать возможность того, что на любом этаже выйдет не наиболее 1-го пассажира.

Решение. При решении предполагаем, что различные методы распределения пассажиров по этажам равновероятны. Разумеется, любой пассажир имеет четыре способности для выхода из лифта (на 2, 3, 4, 5 этажах). Тогда для 2-ух пассажиров имеется способностей, другими словами разных вариантов выхода из лифта, потому что любая возможность выхода первого пассажира может сочетаться с каждой возможностью второго. Для 3-х пассажиров 4*4*4=64 вариантов выхода. Итак, , это число всех вероятных равновероятных (по допущению) методов выхода пассажиров из лифта, один и лишь один из которых будет реализован в итоге тесты. Число вариантов определяющих интересующее нас событие, другими словами равно 4*3*2 исходов, . Потому что на любом этаже обязано выйти не наиболее 1-го пассажира, то у первого выходящего имеется 4 варианта выхода (на любом, не считая первого, этаже), у второго – лишь 3 варианта, потому что один вариант употреблял 1-ый пассажир, у третьего – лишь 2 метода. совсем: возможность действия А равна .

Зарождение теории вероятностей и формирование первых понятий данной для нас ветки арифметики вышло посреди 17 века, когда Паскаль, Ферма, Бернулли попробовали выполнить анализ задач связанных с азартными играми новенькими способами. Скоро сделалось ясно, что возникающая теория отыщет широкий круг внедрения для решения почти всех задач возникающих в разных сферах деятель человека.

Перечень литературы

В.Е. Гмурман Теория вероятностей и математическая статистика. М., ВШ, 1977.

Л.В. Тарасов мир, построенный на вероятности. М., Пр., 1984.

]]>