Учебная работа. Реферат: Геометрия пространства двойной планетной системы: Земля — Луна

Учебная работа. Реферат: Геометрия пространства двойной планетной системы: Земля — Луна

И.В. Злобин

Член Финляндской Астрономической Ассоциации,Хельсинки, Финляндия

В данной работе рассмотрен процесс стойкости Луны на орбите вокруг Земли, исходя из убеждений геометродинамики. Представлено предложение, в каком формулируется догадка о существовании гравитационного «барьера» меж Землей и Луной. Способом диаграмм погружения количественно определена высота предполагаемого «барьера» в точке пересечения искривленных метрик; так, высота «барьера» со стороны Луны оценивается величиной см , а со стороны Земли см. Проведена оценка времени соскальзования Луны со собственной орбиты, в итоге торможения вызванного излучением слабеньких гравитационных волн. Оказалось, что сек

1. Введение

задачка о устойчивом движении естественного спутника Земли является одной из самых сложных в небесной механике. Это вызвано последующими обстоятельствами: 1) Луна — самое близкое к Земле небесное тело мельчайшие неправильности в движении Луны могут быть увидены с Земли; 2) изменение положения Луны относительно Земли происходит: во-1-х — за счет притяжения ее Землей (основная сила) и во-2-х — за счет того, что солнце притягивает Луну слабее либо посильнее, чем землю, т.к. Луна оказывается (в процессе движения по орбите вокруг Земли) то поближе, то далее от Солнца по сопоставлению с Землей, т.е. вследствие разности сил притяжения Солнцем Земли и Луны; 3) Земля не является четким шаром, она имеет форму — сфероида. Но, возмущающая сила за счет сжатия не превосходит 10 — 6
силы притяжения меж Луной и Землей [ 1 ]; 4) Луна {перемещается} в пространстве по орбите глубоко снутри сферы деяния Земли.

сейчас, теория движения Луны основывается на представлениях ньютоновской механики и оперирует законами традиционной физики. Внедрение этих законов дозволяет довольно буквально обрисовывать 2. Теоретическая часть.

До этого, чем перейти к анализу примем ряд допущений: 1) планетка Земля и ее естественный спутник Луна — есть по необходимости сферические симметричные системы.. Это обусловленно тем, что можно пренебречь малостью возмущающей силы, которая возникает за счет степени сжатия Земли и Луны. Как следует, создаваемые этими объектами гравитационные поля должны владеть сферически симметричной топологией; 2) расчет будем проводить для определенного статического положения, т.е. для фиксированной в пространстве и во времени координатной точки расположенной на орбите Луны; 3) квантовыми флуктуациями метрики возникающими поблизости выше обозначенных объектов пренебрегаем.

Итак, приняв за базу, что Земля и Луна в нашем случае являются сферическими симметричными системами, то к системам такового рода можно применить аксиому Биргоффа [2], которая формулируется последующим образом: неважно какая сферически симметричная геометрия некой области пространства-времени (являющаяся решением уравнения Эйнштейна в вакууме) с необходимостью является частью геометрии Шварцшильда. Таковым образом, сферически симметричное гравитационное поле в пустом пространстве обязано быть статическим и описываться метрикой Шварцшильда [3]

, (1)

где угловой элемент. При этом, тут принята метрика с сигнатурой (+ ; -;-;-). Так же, понятно, что в данном случае поля тяготения создаются конкретно Землей и Луной.

Понятно, что неважно какая неоднородность в пространстве, вызванная наличием начальных масс, ведет к возмущению пространственно-временной метрики. вопросец заключается в том, на сколько то либо другое тело «деформирует» геометрию места? тут, необходимо подчеркнуть, что глубина гравитационной ямы прямо пропорциональна массе М стоящей под знаком радикала. Это значит, что для хоть какого текущего значения М можно расчитать характеристики гравитационной возможной ямы.

Для того, чтоб получить численные значения глубин гравитационных ям, нужно пользоваться выводами, вытекающими из геометродинамики [3]. В ее базе лежат законы, которые используются для анализа мощных гравитационных полей, т.е. для объектов с довольно большенными массами. задачка данного исследования сводится к том, чтоб применить методику применяющуюся в геометродинамики конкретно к поля тяготения создаваемые Луной и Землей. законы геометродинамики не ограничивают внедрения ее правил для анализа слабеньких гравитационных полей.

Понятно, что начальная двойная планетная система Земля-Луна владеет неспешным движением и слабеньким гравитационным полем, это подтверждается неравенствами [4]

(2)

где М — масса системы, R — радиус системы, v — скорость снутри системы, 2GM /с2
— радиус Шварцшильда, с — скорость света. К тому же, как отмечается в [5], из предложения о малой скорости вытекает условие, что само гравитационное поле обязано быть слабеньким. В связи с сиим, планетка Земля и ее естественный спутник делают вокруг себя искривление пространства-времени, но кривизна метрики будет маленький.

Сформулируем такое предложение

Для того, чтоб величины и имели достоверный нрав, нужно и довольно, получить полное согласование расчетных данных с выводами как с ньютоновской концепцией тяготения, так и с эйнштейновской теорией гравитации.

Для раскрытия сути предложения воспользуемся одним из правил геометродинамики, а конкретно, способом диаграмм погружения. Мысль этого способа заключается в том, чтоб для погруженной поверхности [3] с неизменными t и г нужно отыскать функцию Z (г) такую, для которой

(3)

Решение имеет вид

(4)

Соотношение (4) представляет собой параболоид, приобретенный методом вращения параболы вокруг оси г . В выражение (4) входят: масса объекта М , имеющая размерность — см ; радиус-вектор г — единицы измерения, которого тоже см . Оба этих параметра имеют размерность выраженную через геометризованные единицы [6] .

С физической точки зрения нужно отметить и таковой факт: диаграммы погружения для планет (звезд) строятся, как для внутренних областей, так и для наружных. Но для передвигающихся частиц (тел) не имеет значения какова геометрия снутри планетки (звезды), так как частичка (тело) никогда не попадет вовнутрь планетки (звезды); до этого чем, это произойдет будет наблюдаться процесс столкновения с поверхностью планетки (звезды), очевидно в том случае, если центром притяжения является планетка (звезда).

3. Результаты

До этого чем, перейти к вопросцам расчетного нрава, нужно сказать последующее: т.к. в геометродинамике все величины переводятся в геометризованные единицы, как следует и тут нужно за ранее скорректировать физические характеристики Луны и Земли. Для того, чтоб привести физическую массу выше обозначенных объектов к геометризованной воспользуемся выражением вида [4]

(5)

где Mgeom
— приведенная масса тела, Mphys
— физическая масса тела, G — гравитационная неизменная, с — скорость света. Физическая масса Земли и Луны определяются, как г и г соответственно. сейчас воспользовавшись (5) оценим приведенные геометризованные массы Луны и Земли: см , см.

При построении диаграмм погружения, следует учесть, что текущее имеет пространство действительная область шварцишльдовской геометрии, а при г < 2М — геометрия становится сингулярной.

Для определения координат диаграмм погружения подставляем и, а так же варьированные значения г в (4) при этом дляпростоты расчетов будем выражать текущие значения радиус-вектора через текущие значения приведенных масс Земли и Луны соответственно, см. формулу (4). Приобретенные результаты занесены в Таблицы 1 и 2.

Таблица 1

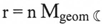
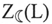
см
n
см

0,01090
2
0

0,01635
3
0,0154142

0,02180
4
0,0217990

0,02725
5
0,0266983

0,03270
6
0,0308285

0,03815
7
0,0344688

0,04360
8
0,0377584

0,04905
9
0,0407835

0,05450
10
0,0435993

Таблица 2

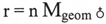
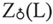
см
n
см

0,874
2
0

1,311
3
1,2360226

1,748
4
1,6748000

2,185
5
2,1408540

2,622
6
2,4720453

3,059
7
2,7638306

3,496
8
3,0276248

3,933
9
3,2702085

4,37
10
3,4960000

В данном анализе этого довольно для того, чтоб выявить конфигурацию диаграмм.. На Рисунках 1 и 2 показаны гравитационные «профили» погруженных поверхностей.

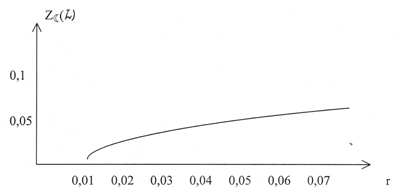
Рис. 1.

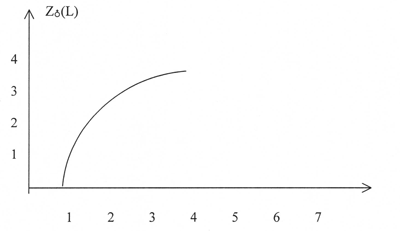
Рис. 2.

Последующим шагом является выявление инвариантности меж радиус-вектором г и средним расстоянием L меж Землей и Луной. Вправду, радиус-вектор г — это, по суте дела, текущее расстояние от тела до случайной координатой точки в пространстве. Таковым образом, просто увидеть, что L тождественно некому текущему значению г . Понятно, что среднее расстояние от Зумли до Луны оценивается в 384400 км [7]. Запишем L в системе СГС, получаем: см . Подставляя L в (4) и беря во внимание соотношение значений и находим, что глубина гравитационной ямы равна:со стороны Земли см,со стороны Луны см.

Последующим шагом является определение координат точки, являющейся местом пересечения 2-ух диаграмм погружения. Обозначим эту точку через А ; примем так же, что А владеет единичной массой mA
. Каким свойствам обязана подчиняться эта точка:

1) т. А будет размещаться меж орбитами Луны и Земли на таком расстоянии, на котором сила тяготения от Земли до А и сила тяготения от Луны до А — адекватны, т.е.; при всем этом и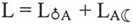

2) т. А размещается на верхушке гребня 2-ух пересеченных метрик, т.е. она будет являться наивысшей точкой «барьера», высоту которого обозначим через h.

Проведем проработку пт 1 и 2 , для этого используем (Рис.3).

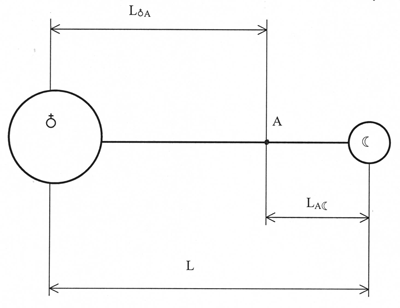
Рис 3.

По пт 1 запишем законглобального тяготения для т. А , Земли и Луны. Имеем:

со стороны Земли (6)

со стороны Луны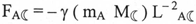

С учетом равентсва этих сил, получим

(7)

где — гравитационная неизменная; г — физическая масса Земли, г — физическая масса Луны; mA
— единичная масса т. А ; — расстояние от Земли до т. А ; — расстояние от т. А до Луны. Потому что, как следует выражение (7) перепишется в виде

(8)

Это соотношение разрешимо относительно, если;.Опосля преобразований находим, что

(9)

Отсюда см . Тогда и см . Проверка: в выражение (6) подставляем и и выясняем, что;. Видно, что значения гравитационных сил согласуется до 4-ого знака опосля запятой.

сейчас, остается подставить и, которые тождественны г , в (4) , чтоб найти величину параметра h , обозначенного в пт 2) . Таковым образом, со стороны Луны т. А размещается на высоте, а со стороны Земли смПерейдем сейчас к вопросцу, который касается задачи связанной с действием гравитационного излучения начальной двойной системы. Естественно ждать, что при тех параметрах, которыми владеет двойная планетная система Земля-Луна полная энергия излучения Е и мощность Р будут определяться очень малыми значениями. В данной работе не проводятся численные оценки этих характеристик, ибо это не заходит в задачку данного исследования. тут, просто, констатируется выше обозначенный факт.

Из всего комплекса черт описывающих процесс гравитационного излучения двойной системы, заслуживает внимание лишь время t, через которое расстояние меж Землей и Луной уменьшится до нуля [3]

(11)

где L — расстояние меж Землей и Луной; — масса, равная

— масса, равная

. Беря во внимание их численные значения, которые указаны в (5), находимсм . Используя калибровку вида [4]

(12)

определяем, что время, выраженное в физических единицах, при котором расстояние меж Луной и Землей уменьшится до нуля, равно сек . Таковым образом, двойная планетная система Земля-Луна будет устойчива на большенном временном промежутке, даже в случае излучения слабеньких гравитационных волн.

Согласно предложенному сценарию строения межпланетной геометрии места двойной системы Земля-Луна, смотрим последующую картину (Рис. 4).

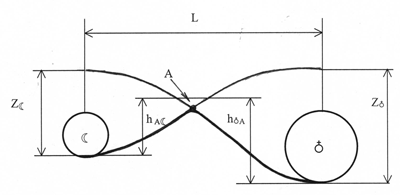
Рис.4

Пусть, некое пробное тело движется от Земли к Луне. Тогда, оно будет подниматься по геодезической из возможной гравитационной ямы Земли по направлению к верхушке «барьера» метрики (т. А). По мере движения ввысь по «барьеру» пробное тело испытывает уменьшение действия поля тяготения Земли. На верхушке «барьера» действие гравитационных сил со стороны Луны и Земли идиентично. Соскальзывая с «барьера» (процесс погружения ), пробное тело все больше захватывается возможным гравитационным полем Луны. Спустившись с «барьера» метрики оно оказывается в гравитационной яме, сделанной Луной.

4. Заключение.

В данной работе, используя методику диаграмм погружения, были определены: 1) глубины возможных гравитационных ям создаваемые Землей и Луной соответственно; 2) найдены определенные значения высоты пространственного «барьера», как со стороны Луны —, так и со стороны Земли —. Как и предполагалось, эти числовые свойства малы в соизмерении, как с расстоянием L меж Землей и Луной, так и с самими размерами этих тел [4] (радиус Земли равен см, а радиус Луны — см). Данный факт находится в неплохом согласии с механикой Ньютона, которая применяется для анализа слабеньких источников гравитационных полей.

Может быть, наличие «барьера» метрики меж Землей и Луной в доборной степени содействует стойкости в пространстве начальной двойной планетной системы. Хотя высота этого «барьера» и ерундова, но Луна, просто не может преодолеть этот «барьер» без наружного притока доборной энергии, таковой, при которой Луна смогла бы подняться на верхушку «барьера» и скатиться по искривленному профилю метрики в центр возможной гравитационной ямы создаваемой Землей.

Отсутствие же «пространственного барьера», по всей видимости, может привести к неуравновешенному состоянию двойной планетной системы Земля — Луна . Отмечается так же, что отысканные характеристики и будут нужны для наиболее тонких оценок физико-геометрического состояния искривленного места в выше обозначенной системе.

Отметим так же, что предложенное в данном работе исследование не заменяет собой строгие традиционные выводы объясняющие устойчивое положение на орбите естественного спутника Земли. Оно дозволяет поглубже посмотреть на механизм гравитационной связанности Луны и Земли.

И в окончании, хотелось бы отметить два очень принципиальных следствия, которые вытекают из анализа представленного в данной статье:

1) потому что, Луна движется вокруг Земли по эллиптической орбите, т.е. имеется апогей (406700 км) и перигей (356400км), то просто увидеть, что высота гравитационного «барьера» h будет варьироваться от min до max величины. При этом min высота достигается при апогее, a max — при перигее. Численные значения планируется получить в новеньком исследовании;

2) аппроксимируя методику диаграмм погружения в целом на всю Галлактику можно буквально выстроить гравитационный профиль нашей планетной системы, что, так же, в перспективе отыщет отражение в будущих работах.

Перечень литературы

Ю.А. Рябов, движение небесных тел, Наука, Москва (1977).

G. D. Birkhoff, Relativity and modern physics, Mass., Harvard University Press, Cambridge, (1923).

А. Лайтман, В. Пресс, Р. Прайс, С. Тюкольский, Сборник задач по теории относительнотси и гравитации, пер. с англ. А. П. Бондарев и Ю. А.Данилов, под ред. И. М. Халатникова, мир, Москва, (1979).

К. R. Lang, Astrophysical formulae, Part 2, Springer-Verlad , Berlin, Heidelberg, New York, (1974)

Л. Д. Ландау, Е. М. Лифшиц, Теория Поля, Наука, Москва, (1973).

С. W. Misner, К. S. Thorn, J. A. Wheeler, Gravitation, W. H. Freeman, New York, (1973).

М. У. Сагитов, Лунная гравиметрия, Наука, Москва, (1979).

]]>