Учебная работа. Реферат: Формула полной вероятности

Учебная работа. Реферат: Формула полной вероятности

.

Пусть имеется группа событий H1
, H2
,…, Hn
, владеющая последующими качествами:

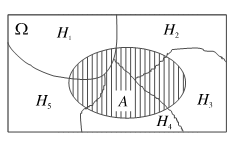
1) все действия попарно несовместны: Hi
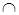Hj
=Æ; i, j=1,2,…,n; i¹j;

2) их объединение образует место простых исходов W:

W=.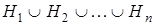

Рис.8

В этом случае будем гласить, что H1
,H2
,…,Hn
образуют полную группу событий. Такие действия время от времени именуют догадками.

Пусть А – некое событие: А ÌW (диаграмма Венна представлена на рисунке 8). Тогда имеет пространство формула полной вероятности:

P(A) = P(A/ H1
)P(H1
) + P(A/ H2
)P(H2
) + …+ P(A/ Hn
)P(Hn
) =

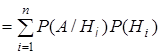
подтверждение. Разумеется: A = 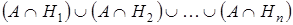, при этом все действия 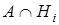(i = 1,2,…,n) попарно несовместны. Отсюда по аксиоме сложения вероятностей получаем

P(A) = P(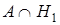) + P(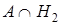) +…+ P(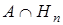

Если учитывать, что по аксиоме умножения P(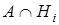)= P(A/Hi
)P(Hi
) (i=1,2,…,n), то из крайней формулы просто получить приведенную выше формулу полной вероятности.

Пример. В магазине продаются электролампы производства 3-х заводов, при этом толика первого завода — 30%, второго — 50%, третьего — 20%. Брак в их продукции составляет соответственно 5%, 3% и 2%. Какова возможность того, что случаем избранная в магазине лампа оказалась бракованной.

Пусть событие H1
заключается в том, что избранная лампа произведена на первом заводе, H2
на втором, H3
— на 3-ем заводе. Разумеется:

P(H1
) = 3/10, P(H2
) = 5/10, P(H3
) = 2/10.

Пусть событие А заключается в том, что избранная лампа оказалась бракованной; A/Hi
значит событие, состоящее в том, что выбрана бракованная лампа из ламп, сделанных на i-ом заводе. Из условия задачки следует:

P (A/H1
) = 5/10; P(A/H2
) = 3/10; P(A/H3
) = 2/10

По формуле полной вероятности получаем

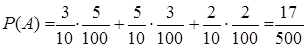
Формула Байеса

Пусть H1
,H2
,…,Hn
— полная группа событий и АÌW – некое событие. Тогда по формуле для условной вероятности

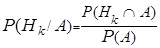
тут P(Hk
/A) – условная возможность действия (догадки) Hk
либо возможность того, что Hk
реализуется при условии, что событие А вышло.

По аксиоме умножения вероятностей числитель формулы

можно представить в виде

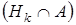P = P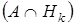= P(A /Hk
) P(Hk
)

Для представления знаменателя формулы

можно применять формулу полной вероятности

P(A)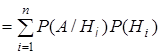

сейчас из

можно получить формулу, именуемую формулой Байеса:

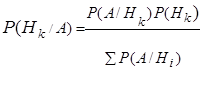
По формуле Байеса исчисляется возможность реализации догадки Hk
при условии, что событие А вышло. Формулу Байеса еще именуют формулой вероятности гипотез. Возможность P(Hk
) именуют априорной вероятностью догадки Hk
, а возможность P(Hk
/A) –апостериорной вероятностью.

Пример. Разглядим приведенную выше задачку о электролампах, лишь изменим вопросец задачки. Пусть клиент купил электролампу в этом магазине, и она оказалась бракованной. Отыскать возможность того, что эта лампа сделана на втором заводе. Величина P(H2
) = 0,5 в данном случае это априорная возможность действия, состоящего в том, что приобретенная лампа сделана на втором заводе. Получив информацию о том, что приобретенная лампа бракованная, мы можем поправить нашу оценку способности производства данной нам лампы на втором заводе, вычислив апостериорную возможность этого действия.

Выпишем формулу Байеса для этого варианта

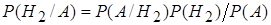
Из данной нам формулы получаем: P(H2
/A) = 15/34. Как видно, приобретенная информация привела к тому, что возможность интересующего нас действия оказывается ниже априорной вероятности.

задачки с решениями.

1.В первой урне 7 белоснежных и 3 темных шара, во 2-ой – 8 белоснежных и 2 темных. При перевозке из первой урны во вторую урну перекатились два шара. Опосля того, как шары во 2-ой урне перемешались, из неё выкатился шар. Отыскать возможность того, что выкатившийся из 2-ой урны шар белоснежный.

Пусть событие Н1
заключается в том, что из первой урны во вторую перекатились два белоснежных шара, событие Н2
заключается в том, что перекатились два чёрных шара, а событие Н3
заключается в том, что перекатились шары различного цвета. Можно вычислить вероятности Р(Н1
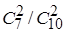)==7/15, Р(Н2
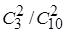)==1/15, Р(Н3
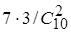)==7/15 (при решении задачки полезно проверить выполнение нужного условия ).

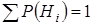Если реализовалась догадка Н1
, то во 2-ой урне оказалось 10 белоснежных и 2 темных шара. Обозначим через А событие, заключающееся в том, что из 2-ой урны выкатился белоснежный шар. Тогда Р(А/Н1
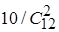)==5/33. Если реализовалась догадка Н2
, то во 2-ой урне оказалось 8 белоснежных и 4 чёрных шара, и Р(А/Н2
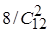)==4/33. Просто показать, что Р(А/Н3
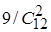)==3/22. сейчас можно пользоваться формулой полной вероятности:

Р(А)=(5/33)×(7/15)+(4/33) (1/15)+(3/22) (7/15)=47/330

2. В условие задачки №1 внесем изменение. Пусть опосля того, как из первой урны во вторую перекатились два шара и шары во 2-ой урне перемешались, из неё выкатился белоснежный шар. Отыскать возможность того, что из первой урны во вторую перекатились разноцветные шары.

Вычисления предшествующей задачки подставим в формулу Байеса

Р(Н3
/А)=Р(А/Н3
)Р(Н3
)/ Р(А)=(3/22)(7/15)/( 47/33)=7/47

3. В ящике лежат 20 теннисных мячей, в том числе 15 новейших и 5 играных. Для игры выбираются 2 мяча и опосля игры ворачиваются назад. Потом для 2-ой игры также наудачу извлекаются ещё два мяча. Отыскать возможность того, что 2-ая игра будет проводиться новенькими мячами.

Обозначим через А событие, заключающееся в том, что 2-ая игра будет проводиться новенькими мячами. Пусть догадка Н1
заключается в том, что для первой игры были выбраны два новейших мяча, догадка Н2
заключается в том, что для первой игры были выбраны новейший и играный мячи, догадка Н3
заключается в том, что для первой игры были выбраны два играных мяча. Определим вероятности гипотез:

Р(Н1
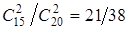)=; Р(Н2
)=; Р(Н3
)=.

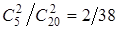сейчас вычислим условные вероятности действия А.

Р(А/Н1
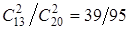)=; Р(А/Н2
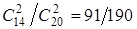)=; Р(А/Н3
)=.

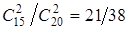Осталось подставить результаты вычислений в формулу полной вероятности

Р(А)=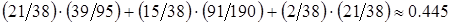

4. Сообщение со спутника на землю передаётся в виде бинарного кода, другими словами как упорядоченного набора нулей и единиц. Представим, что послание на 70% состоит из нулей. Помехи приводят к тому, что лишь 80% нулей и единиц верно распознаются приёмником. Если принят сигнал “1”, то какова возможность того, что выслан сигнал “0”?

Пусть событие В0
заключается в том, что выслан сигнал “0”, а событие В1
–в том, что выслан сигнал “1”. Пусть событие А0
заключается в том, что принят сигнал “0”, с событие А1
– в том, что принят сигнал “1”. Нас интересует Р(В0
/А1
). По условию

Р(В0
)=0,7 Р(В1
)=0,3

Р(А0
/ В0
)=0,8 Р(А1
/ В0
)=0,2

Р(А1
/В0
)=0,8 Р(А0
/ В 1
)=0,2

По формуле Байеса получаем

Р(В0
/А1
)=0,2×0,7/(0,2×0,7+0,8×03)=0,37.

5. Бригада, работающая в дневную смену, производит изделий вдвое больше, чем бригада, работающая в ночную смену. Отсюда следует, что если избрать случайным образом изделие, произведённое в цеху, то с вероятностью 2/3»0,66 оно произведено бригадой, работающей днём. Это априорная возможность. Понятно, что бригада, работающая днём, производит 3% некондиционных изделий, а бригада, работающая ночкой, – 7% некондиционных изделий. Пусть случайным образом отобранное изделие оказалось некондиционным. Тогда по формуле Байеса можно вычислить апостериорную возможность того, что это изделие произведено дневной бригадой

P(Н1
/А)=(3/100)(2/3)/((3/100)(2/3)+(7/100)(1/3))»0,632

Как видно, апостериорная возможность интересующего нас действия тут несколько ниже априорной вероятности.

Задачки для самостоятельного решения.

1) Для проверки усвоения лекционного материала в студенческой группе был случайным образом избран студент, и ему был предложен тест по теме лекции. В данной нам студенческой группе 6 отличников, 7 добротных студентов и три средних студента (по результатам прошедшей сессии). Было понятно, что отличник совладевает с тестом с вероятностью 0,85, неплохой студент совладевает с тестом с вероятностью 0,6, а средний студент совладевает с тестом с вероятностью 0,3.

а) вычислить априорную возможность того, что был протестирован неплохой студент;

в) вычислить возможность того, что студент не совладал с тестом;

с) вычислить возможность того, что был избран неплохой студент, если понятно, что студент с тестом не совладал.

2) В упаковке находилось 7 изделий первого сорта и 5 изделий второго сорта, снаружи неразличимых. При транспортировке два изделия были похищены. Опосля этого из упаковки было извлечено наудачу изделие и подвергнуто проверке на свойство.

а) вычислить возможность того, что были похищены изделия второго сорта;

в) вычислить возможность того, что посреди похищенных изделий одно было первого сорта, другое второго сорта;

с) вычислить возможность того, подвергнутое проверке изделие было второго сорта;

d) вычислить возможность того, что похищенные изделия были второсортными, если

Ответы. 1) а) 7/16=0,4375; в) 0,3625 с) 0,482759.

]]>