Загрузка...
Учебная работа. Реферат: Приближенное вычисление определенного интеграла при помощи квадратурной формулы Чебышева
МИНИСТЕРСТВО ОБРАЗОВАНИЯ УКРАИНЫ
ГОСУДАРСТВЕННЫЙ ХИМИКОТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ техники
Днепропетровск 2000г.
1. Общая постановка и анализ задачки.
1.1. Введение.
Требуется отыскать определенный интеграл
I =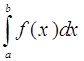 
по квадратурной формуле Чебышева.
Разглядим, что представляет из себя совершенно квадратурная формула, и как можно с ее помощью вычислить приближенно интеграл.
Понятно,
что определенный интеграл функции 
типа 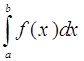численно представляет собой площадь криволинейной трапеции ограниченной кривыми x=0, y=a, y=b и y= (Рис.1).
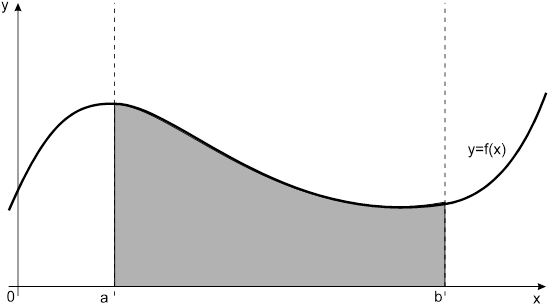
Рис. 1. Криволинейная трапеция.
Если f(x) непрерывна на отрезке [a, b], и известна ее первообразная F(x), то определенный интеграл от данной функции в границах от а до b быть может вычислен по, известной всем, формуле Ньютона — Лейбница
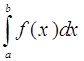= F(b) — F(a)
где
F’(x) = f(x)
Но в почти всех вариантах F(x) не быть может найдена, либо первообразная выходит весьма сложной для вычисления.
Не считая того, функция нередко задается таблично. Потому огромное
задачка численного интегрирования состоит в нахождении приближенного значения интеграла 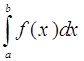по данным либо вычисленным значениям подинтегральной функции f(x) в неких точках ( узлах ) отрезка [ a, b].
Численное определение однократного интеграла именуется механической квадратурой, а надлежащие формулы численного интегрирования — квадратурными .
Заменяя подинтегральную функцию любым интерполционным многочленом, мы получим квадратурные формулы вида
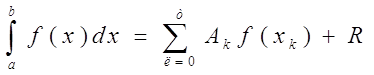
где
xk — избранные узлы интерполяции;
Ak — коэффициенты, зависящие лишь от выбора узлов, но
не от вида функции (k=0,1,2,…….., n).
R — остаточный член, либо погрешность квадратурной формулы.
Отбрасывая остаточный член R, мы совершаем погрешность усечения.
При расчете к ней добавляются еще разные погрешности округления.
Разобьем отрезок интегрирования [a, b] на n равных частей системой точек
xi= xo+ i..h; ( i = 0,1,2,……,n)
xo= a; xn= b;
h= (b-a)/n ;
и вычислим подинтегральную функцию в приобретенных узлах
yi= f(xi) ; ( i = 0,1,2,……,n)
1.2. Вывод формул численного интегрирования с внедрением интерполяционного полинома Лагранжа
Пусть для y=f(x) известны в n+1 точках X0,X1,X2..Xn промежутка [a,b] надлежащие значения f(xi)=yi (i=0,1,2..n). Требуется приближенно отыскать
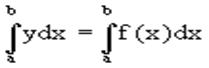
По данным значениям Yi построим полином Лагранжа. Заменим f(x) полиномом Ln(x). Тогда
где Rn(f) – ошибка квадратурной формулы. Отсюда, воспользовавшись выражением для Ln(x), получаем приближенную квадратурную формулу:
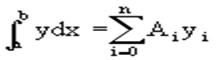
Для вычисления коэффициентов Аi заметим что:
1.коэффициенты Ai при данном расположении узлов не зависит от выбора функции f(x);
2.для полинома степени n крайняя формула четкая.
Пологая y=xK (k=0,1,2..,n), получим линейную систему из n+1 уравнений:
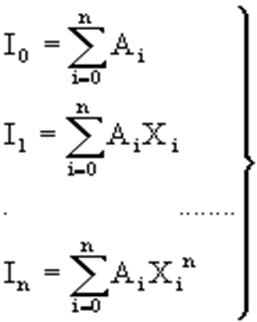
где
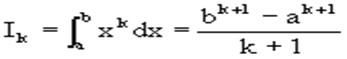
(k=0,1,..,n), из которой можно найти коэффициенты А0,А1,..,АN.
Определитель системы есть определитель Вандермонда
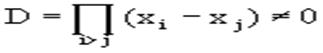
Заметим, что при применении этого способа фактическое построение полинома Лагранжа Ln(x) является лишним. Обычной способ подсчета погрешности квадратурных формул разработан С.М. Никольским.
сейчас разглядим несколько простых квадратурных формул :
1.3 Формула трапеций и средних прямоугольников.
Заменим дугу АВ стягивающей ее хордой, получим прямолинейную трапецию аАВb, площадь которой примем за приближенное
B
y
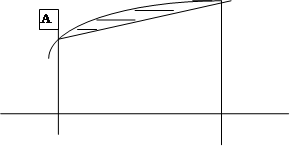
0 a b x
рис 1.3.1 Криволинейная трапеция
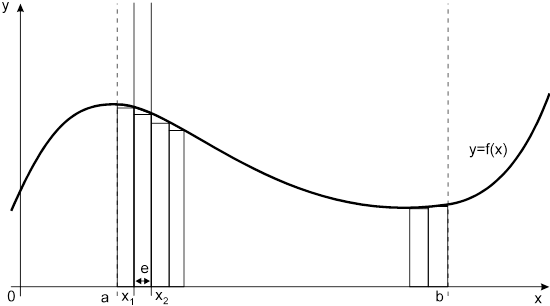
Рис. 1.3.2. способ трапеций.
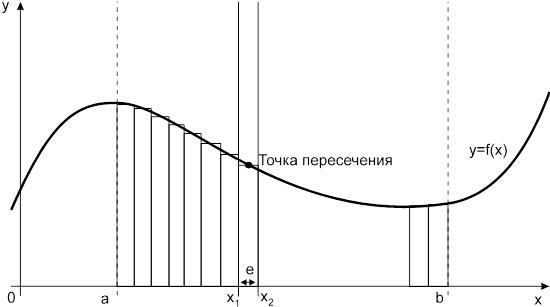
Рис. 1.3.3. Способ средних прямоугольников.
По способам трапеций и средних прямоугольников соответственно интеграл равен сумме площадей прямоугольных трапеций, где основание трапеции какая-либо малая величина (точность), и сумма площадей прямоугольников, где основание прямоугольника какая-либо малая величина (точность), а высота определяется по точке пересечения верхнего основания прямоугольника, которое график функции должен пересекать посреди. Соответственно получаем формулы площадей —
для способа трапеций:
,
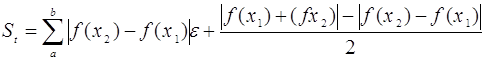для способа средних прямоугольников:
.
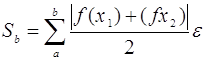1.4. Общая формула Симпсона (параболическая формула)
Пусть n=2m есть четное число и yi=f(xi) (i=0,1,2…n) — значения функции y=f(x) для равноотстоящих точек а=x0,x1, … ,xn=b с шагом
Применив формулу Симпсона к любому удвоенному промежутку [x0,x2], [x2,x4] … [x2m-2,x2m] длины 2h и введя обозначения
s1=y1+y2+ … +y2m-1
s2=y2+y4+ … +y2m
получим обобщенную формулу Симпсона:
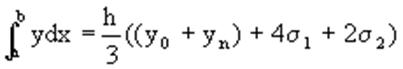
Остаточный член формулы Симпсона в общем виде:
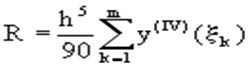
где xk I (x2к-2,x2к)
1.5. Квадратурная формула Чебышева
Разглядим квадратурную формулу вида:
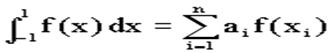
функцию f(x) будем исать в виде когда f(x) многочлен вида f(x)=ao+a1x+…+anxn . Проинтегрировав, преобразовав и подставив значения многочлена в узлах
f(x1)=a0+a1x1+a2x12+a3x13+…+anx1n
f(x2)=a0+a1x2+a2x22+a3x23+…+anx2n
f(x3)=a0+a1x3+a2x32+a3x33+…+anx3n
. . . . . . . . . . . . . . . .
f(xn)=a0+a1xn+a2xn2+a3xn3+…+anxnn
получим формулу Чебышева.
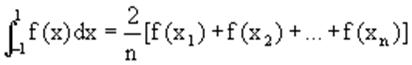
значения х1,х2,..,хn для разных n приведены в таблице 3.
Таблица 3 – значения х1,х2,..,хn для разных n.
n
I
ti
n
i
ti
2
1;2
± 0,577350
6
1;6
± 0,866247
3
1;3
± 0,707107
2;5
± 0,422519
2
0
3;4
± 0,266635
4
1;4
± 0,794654
7
1;7
± 0,883862
2;3
± 0,187592
2;6
± 0,529657
5
1;5
± 0,832498
3;5
± 0,321912
2;4
± 0,374541
4
0
3
0
2. Решение контрольного примера
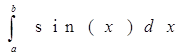
где a=0 ; b= 
; при n=5;
f(x) = sin(x);
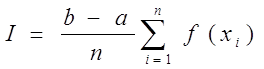
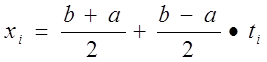
i
xi
yi
1
0,131489
0,131118
2
0,490985
0,471494
3
0,785
0,706825
4
0,509015
0,487317
5
0,868511
0,763367
x1= p/4+p/4*t1=p/4+p/4(-0,832498)=0,131489
x2= p/4+p/4*t2=p/4+p/4(-0,374341)=0,490985
x3= p/4+p/4*t3=p/4+p/4*0=0,785
x4=1- x2=1-0,490985 = 0,509015
x5=1- x1=1-0,131489=0,868511
y1=sin(x1) = sin(0,131489)=0,131118
y2=sin(x2) = sin(0,490985)=0,471494
y3=sin(x3) = sin(0,785)=0,706825
y4=sin(x4) = sin(0,509015)=0,487317
y5=sin(x5) = sin(0,868511)=0,763367
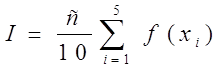
I = p/10(0,131118+0,471494+0,706825+0,487317+0,763367) =
=p/10*2,560121=0,8038779.
3. Описание программки Integral. pas. метод.
Процедура VVOD — заполняет массив, содержащий внутри себя аргументы xi
Процедура FORM — используя массив, содержащий аргументы xi заполняет массив yi
Процедура CHEB — используя массивы xi и yi, высчитывает по квадратурной формуле Чебышева приближенное
Процедура TABL — это подпрограмма, осуществляющая вывод таблицы узлов (аргумент — функция)
При запуске программки необходимо ввести границы интегрирования.
Опосля ввода границ интегрирования употребляется процедура VVOD, а потом высчитывается и выводиться на экран шаг табулирования функции h.
Опосля этого используем процедуры FORM и CHEB .
Получив итог, выводим таблицу ( процедура TABL ) и интеграл.
4. Заключение и выводы.
Таковым образом разумеется, что при вычислении определенных интегралов при помощи квадратурных формул, а а именно по формуле Чебышева не дает нам четкого значения, а лишь приближенное.
Чтоб очень приблизиться к достоверному значению интеграла необходимо уметь верно избрать способ и формулу, по которой будет вестись расчет. Так же весьма принципиально то, какой будет взят шаг интегрирования.
Хотя численные способы и не дают весьма четкого значения интеграла, но они весьма важны, потому что не постоянно можно решить задачку интегрирования аналитическим методом.
Листинг программки.
программка написана на языке Tubro Pascal 7.0 для MS-DOS. Ниже приведен ее листинг:
program integral;
uses crt;
const n=5;
k=-0.832498;
l=-0.374541;
z=0.0;
type aa=array[1..n] of real;
var x,y:aa;
a,b,h,ich:real;
{ наполнение х-сов в массив х[5] }
procedure vvod(var a,b:real;var c:aa);
var i:integer;
t:aa;
Begin
t[1]:=k;
t[2]:=l;
t[3]:=z;
t[4]:=l;
t[5]:=k;
for i:=1 to n-1 do
c[i]:=((b+a)/2+(b-a)/2*t[i]);
for i:=n-1 to n do
c[i]:=1 — c[n+1-i];
end;
{ наполнение y-ков в массиве у[5] }
procedure form(var x:aa; var y:aa);
var i:integer;
Begin
for i:=1 to n do
y[i]:=sin(x[i]); {функция}
end;
{ процедура для расчета интеграла по квадратурной
формуле Чебышева }
procedure cheb(var y:aa;var ich:real);
var i:integer;
Begin
ich:=0;
for i:=1 to n do
ich:=ich+y[i]*h;
end;
{ процедура вывода таблицы}
procedure tabl;
var i:integer;
Begin
writeln(‘ ___________________________________ ‘);
writeln(‘| i | t| x|y |’);
writeln(‘ ___________________________________ ‘);
writeln(‘| 1 |’,k:9:6,’|’,x[1]:9:6,’ |’,y[1]:9:6,’|’);
writeln(‘| 2 |’,l:9:6,’|’,x[2]:9:6,’ |’,y[2]:9:6,’|’);
writeln(‘| 3 |’,z:9:6,’|’,x[3]:9:6,’ |’,y[3]:9:6,’|’);
writeln(‘| 4 |’,l:9:6,’|’,x[4]:9:6,’ |’,y[4]:9:6,’|’);
writeln(‘| 5 |’,k:9:6,’|’,x[5]:9:6,’ |’,y[5]:9:6,’|’);
writeln(‘ ___________________________________ ‘);
end;
Begin
clrscr;
writeln(‘ П Р О Г Р А М М А Д Л Я В Ы Ч И С Л Е Н И Я’);
writeln(‘ О П Р Е Д Е Л Е Н Н О Г ОИ Н Т Е Г Р А Л А ‘);
writeln;
writeln(‘Введите границы интегрирования a,b:’);
readln(a,b);
vvod(a,b,x);
h:=(b-a)/n;
writeln(‘h=’,h:9:6);
form(x,y);
cheb(y,ich);
tabl;
writeln(‘I=’,ich:8:6);
end.
Вывод результата :
П Р О Г Р А М М А Д Л Я В Ы Ч И С Л Е Н И Я
О П Р Е Д Е Л Е Н Н О Г ОИ Н Т Е Г Р А Л А
Введите границы интегрирования a,b:
0 1.5708
h= 0.314160
____________________________
| i | t | x | y |
____________________________
| 1 |-0.832498| 0.131556 | 0.131177|
| 2 |-0.374541| 0.491235 | 0.471716|
| 3 | 0.000000| 0.785400 | 0.707108|
| 4 |-0.374541| 0.508765 | 0.487099|
| 5 |-0.832498| 0.868444 | 0.763325|
____________________________
I=0.804383
Перечень
литературы:
1. Ракитин Т.А., Первушин В.А. “Практическое управление по численным способам с приложением программ на языке Basic“
2. Крылов В.И. “Приближенные вычисления интегралов“ — М. : Физмат.
3. Демидович и Марон “Базы вычислительной арифметики“
4. Копченова и Марон “Вычислительная математика в примерах и задачках”
5. Вольвачев А.Н., Крисевич В.С. Программирование на языке Паскаль для ПЭВМ ЕС. Минск.: 1989 г.
6. Зуев Е.А. язык программирования Turbo Pascal. М.1992 г.
7. Скляров В.А. Знакомьтесь: Паскаль. М. 1988 г.
]]>