Учебная работа. Курсовая работа: История статистики
МГТУ «Станкин»
2003 год
Тема 1. Статистическая сводка. Группировка
Статистическая сводка является вторым шагом статистического исследования опосля наблюдения. Она заключается в том, что первичные материалы, приобретенные в итоге наблюдения, обрабатываются, сводятся вкупе и характеризуются итоговыми обобщающими показателями.
Составными элементами сводки являются: 1) программка сводки; 2) подсчет групповых итогов; 3) оформление конечных результатов сводки в виде таблиц и графиков.
программка статистической сводки содержит список групп, на которые расчленена изучаемая совокупа по определенным признакам, также список характеристик, нужных для свойства каждой группы. Программка сводки имеет, как правило, вид вольных статистических таблиц, которые следует заполнить расчетными данными.
В сводке статистического материала принципиальное звено занимают группировки, потому что обычный подсчет итогов без распределения единиц совокупы на группы по тем либо другим признакам не дает полной свойства объекта исследования.
К статистическим группировкам прибегают при решении последующих задач:
а) анализ структуры исследуемой совокупы;
б) выявление связей и взаимозависимостей меж экономическими явлениями.
Для решения первой задачки строят структурные группировки.
Для решения 2-ой задачки строят аналитические группировки.
Группировки бывают обыкновенные и комбинационные. Обычная группировка появляется по одному признаку, комбинационная — по двум и наиболее признакам. Можно производить группировки как по количественному признаку, так и по атрибутивному. В количественной группировке группировочный признак выражается вариациями чисел. В атрибутивной группировке группировочный признак количественного выражения не имеет, потому что охарактеризовывает свойство изучаемого явления.
В экономико-статистическом анализе делаются группировки как с равными, так и с неравными интервалами. При построении группировки с равными интервалами величину интервала групп определяют по последующей формуле:
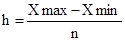 ,
,
где Xmax — наибольшее
При выбирании числа групп нужно учесть последующее: 1) в каждую группу может попасть по способности довольно огромное число единиц; 2) число единиц в группах не обязано резко различаться друг от друга, т.е. обязано быть приблизительно 1-го порядка; 3) групп обязано быть не наиболее 6-7.
Группировки с неравными интервалами целенаправлено использовать в тех вариантах, когда начальные статистические данные разнятся на очень значительную величину, т.е. когда очень велик размах варианты в начальной совокупы.
Разглядим пример на построение аналитической группировки.
Таблица 1.1
Данные о цены главных фондов и товарной продукции компаний
№
п/п
Средняя годичная стоимость главных производственных фондов, млн. руб.
Товарная продукция, млн. руб.
№
п/п
Средняя годичная стоимость главных производственных фондов, млн. руб.
Товарная продукция, млн. руб.
1
396
947,6
11
220
390,1
2
305
602,7
12
318
537,6
3
198
399,6
13
290
436,8
4
386
897,0
14
327
700,0
5
315
642,6
15
208
590,4
6
330
675,0
16
318
591,6
7
205
348,3
17
245
511,8
8
302
582,4
18
340
669,6
9
211
378,3
19
249
537,6
10
306
494,1
20
199
315,0
По отчетным данным 20 промышленных компаний необходимо выстроить аналитическую группировку для установления зависимости размера товарной продукции от средней годичный цены главных производственных фондов (табл. 1.1).
Для построения группировки выделим группировочный признак. Таковым группировочным признаком является средняя годичная стоимость главных производственных фондов. Примем число групп по данному признаку n = 5. Величину интервала в группах определяем по приведенной выше формуле. Тогда h = (396 – 198) : 5 = 39,6 млн. руб.
Образуем группы компаний по средней годичный цены главных производственных фондов. Нижнюю границу первого интервала составит малая величина группировочного признака 198 млн. руб. Верхняя граница первого интервала составит 198 + 39,6 = 237,6 млн. руб.
При группировках по безпрерывно варьирующим количественным признакам границу интервалов обозначают так, что верхняя граница предшествующего интервала служит нижней границей следующего интервала.
Таковым образом, нижней границей второго интервала будет величина 237,6 млн. руб., а верхней границей данного интервала — величина 237,6 + 39,6 = 277,2 млн. руб. Аналогично определяются границы следующих интервалов.
Получаем последующие интервалы для 5 групп компаний по средней годичный цены главных производственных фондов: 198 — 237,6; 237,6 — 277,2; 277,2 — 316,8; 316,8 — 356,4; 356,4 — 396,0. В первую группу вошло 6 компаний; во вторую — 2; в третью — 6; в четвертую — 4; в пятую — 2.
Потому что по условию задачки нужно установить зависимость размера товарной продукции от средней годичный цены главных производственных фондов, то в каждой выделенной группе определяем суммарную величину размера товарной продукции по совокупы компаний в группе и в расчете на одно предприятие.
По первой группе компаний со средней годичный стоимостью главных производственных фондов от 198 млн. руб. до 237,6 млн. руб. размер товарной продукции составит: 399,6 + 348,3 + 378,3 + 350,1 + 590,4 + 315,0 = 2381,7 млн. руб., и в расчете на одно предприятие: 2381,7 : 6 = 396,9 тыс. руб. Подобные расчеты производим по остальным группам.
Результаты расчетов сведем в табл. 1.2.
Таблица 1.2
Расчет среднего размера товарной продукции по группам компаний
Группа компаний по средней годичный цены производственных фондов
Число компаний
Размер товарной продукции, млн. руб.
Размер товарной продукции в среднем 1-го компании в группе, млн. руб.
198 — 237,6
6
2381,7
396,9
237,6 — 277,2
2
1049,4
524,2
277,2 — 316,8
6
3433,6
572,3
316,8 — 356,4
4
2499,8
624,7
356,4 — 396,0
2
1844,6
922,7
На базе построенной группировки видна точная зависимость размера товарной продукции от средней годичный цены главных производственных фондов компании.
Используя условие данной задачки, построим структурную группировку.
Для построения структурной группировки нужно сформировать группы по второму признаку — величине товарной продукции. Возьмем число групп n = 5; границы интервалов групп определяем по формуле величины интервала группировки h, где
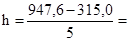 126,52 млн. руб.
126,52 млн. руб.
Группы компаний, образованные по размеру товарной продукции, последующие: 315,0 — 441,52; 441,52 — 568,04; 568,04 — 694,56; 694,56 — 821,08; 821,08 — 947,6.
В предстоящем, осуществляя распределение компаний в группах по средней годичный цены главных производственных фондов на подгруппы по размеру товарной продукции, сформируем структурную группировку (табл. 1.3).
На базе структурной группировки ясно видно распределение компаний по размеру товарной продукции зависимо от той либо другой средней годичный цены производственных фондов.
Таблица 1.3
Структурная группировка компаний по двум показателям
Группа компаний по средней годичный цены ОПФ, млн. руб.
Число компаний
в том числе с объемом товарной продукции, млн. руб.
315,0 — 441,52
441,52 — 568,04
568,04 — 694,56
694,56 — 821,08
821,08 — 947,6
198 — 237,6
6
5
1
237,6 — 277,2
2
2
277,2 — 316,8
6
1
4
316,8 — 356,4
4
1
2
1
356,4 — 396,0
2
2
компании сосредоточены, основным образом, на искосок, что снова подчеркивает наметившуюся тенденцию роста размера товарной продукции при возрастании цены главных производственных фондов компании.
Тема 2. Ряды распределения. Статистические таблицы
В итоге обработки и классификации первичных статистических данных получают ряды цифровых характеристик, которые охарактеризовывают отдельные стороны изучаемых явлений. Эти ряды именуют статистическими.
Статистические ряды делят на два вида: ряды распределения и ряды динамики. Ряды распределения охарактеризовывают распределение единиц совокупы по какому-либо признаку. Ряды динамики охарактеризовывают изменение изучаемых явлений во времени.
Ряды распределения, в свою очередь, делятся на атрибутивные и вариационные. Атрибутивный ряд распределения появляется по высококачественному признаку. Вариационный ряд появляется по количественному признаку.
Посреди вариационных рядов распределения выделяют дискретные и интервальные ряды.
В дискретном вариационном ряду распределения отдельные варианты имеют определенные определенные значения. В интервальном вариационном ряду варианты колеблются в определенных границах. Вариационные ряды изображают в системе прямоугольных координат в виде диаграмм.
Дискретные вариационные ряды изображают в виде так именуемого полигона распределения. Варианты откладываются на оси абсцисс, частоты — на оси ординат. Точки пересечения соединяются отрезками прямой.
Интервальные вариационные ряды изображают в виде гистограммы. На оси абсцисс откладывают границы интервалов, на оси ординат — число единиц совокупы, приходящееся на единицу ширины интервала (плотность распределения). В интервалах строят прямоугольники.
Для изображения интервальных вариационных рядов с равными интервалами на оси абсцисс откладывают границы интервалов, а на оси ординат — число единиц совокупы в данном интервале. Строят прямоугольники с равными интервалами.
Интервальный вариационный ряд можно изображать также в виде кумуляты. На оси абсцисс откладывают границы интервалов, на оси ординат — нарастающие частоты, надлежащие верхним границам интервалов. Точки пересечения соединяют отрезками прямой.
Статистические ряды как итог статистической сводки и группировки постоянно излагаются в виде статистических таблиц.
Статистическая таблица представляет собой форму более оптимального, приятного и систематизированного изложения цифровых результатов сводки и обработки статистического материала.
При построении статистических таблиц следует верно разграничивать статистическое подлежащее и статистическое сказуемое. Статистическим подлежащим таблицы является сам объект (список его единиц либо их групп), который характеризуется числовыми показателями. Статистическим сказуемым таблицы являются числовые характеристики, которые охарактеризовывают изучаемый объект.
Статистическое подлежащее располагают, обычно, в строчках, статистическое сказуемое — в графах таблицы.
Зависимо от строения подлежащего различают три вида таблиц: обыкновенные, групповые, комбинационные.
Обыкновенные (перечневые) таблицы в подлежащем содержат список рассматриваемых объектов.
Групповые таблицы в подлежащем содержат группировку единиц изучаемого объекта, образованную по какому-либо одному признаку.
Комбинационные таблицы в подлежащем содержат группировку единиц, образованную по двум и наиболее признакам.
При построении таблиц следует строго придерживаться определенных правил:
1. Любая таблица обязана быть пронумерована и иметь заголовок, который в короткой форме должен отражать содержание таблицы, пространство и время явления.
2. В таблице употребляются лишь принятые сокращения.
3. В таблице должны быть приведены единицы измерения. Если единица измерения общая, она выносится справа над таблицей в скобках.
4. Цифровые данные целенаправлено сокращать.
5. К таблице можно созодать примечания, которые располагают под таблицей со сноской под чертой.
6. При переносе таблицы на иной лист, графы таблицы целенаправлено обозначать арабскими цифрами.
Тема 3. Графическое изображение статистических данных
Графиками в статистике именуют условные изображения числовых величин и их соотношений в виде разных геометрических фигур в системе прямоугольных координат.
Графики являются средством обобщения и анализа статистических данных. При помощи графиков выявляются главные тенденции развития экономических явлений и обоюдные связи меж явлениями.
Статистические графики различают по содержанию и способу построения.
По содержанию изображаемых статистических характеристик графики делят на последующие виды: 1) графики сопоставления; 2) графики структуры; 3) графики динамики; 4) графики выполнения плана; 5) графики взаимосвязанных характеристик.
По способу построения различают столбиковые, ленточные, линейные, радиальные, квадратные, секторные диаграммы.
Для построения графиков сопоставления целенаправлено применять линейную, столбиковую, ленточную, квадратную, радиальную диаграммы.
Столбиковая диаграмма изображается в виде столбиков, основания которых откладываются на оси абсцисс, высота — на оси ординат. Ширина столбиков случайная, но однообразная.
Линейная диаграмма изображается в виде полосы, соединяющей точки пересечения расчетных величин в ряде динамики.
Ленточную диаграмму целенаправлено строить в том случае, если объект характеризуется 2-мя показателями, как правило, обратными по смыслу. В ленточной диаграмме в отличие от столбиковой столбики размещены не вертикально, а горизонтально в системе прямоугольных координат.
Квадратную диаграмму целенаправлено строить в том случае, когда меж сравниваемыми показателями разница так велика, что установление пригодного масштаба оказывается затруднительным. Сторона всякого квадрата определяется как корень квадратный из соответственной величины. Тогда площадь квадратов зрительно будет охарактеризовывать ту либо иную начальную величину.
Радиальные диаграммы строятся аналогично квадратам. Радиус круга есть корень квадратный из определенной величины.
Для построения графиков структуры, как правило, употребляют столбиковые и секторные диаграммы.
Индивидуальностью построения секторной диаграммы будет то, что размер круга в секторной диаграмме принимается за 100 процентов, а величины секторов пропорциональны процентному отношению составных нередкой к их общему итогу.
Построение графиков динамики осуществляется, как правило, при помощи столбиковой либо линейной диаграмм.
Графическое изображение характеристик выполнения плана можно выполнить в виде линейной, ленточной и столбиковой диаграмм в системе прямоугольных координат. При всем этом на оси абсцисс откладывают периоды динамики, на оси ординат — характеристики выполнения плана.
Для графического изображения характеристик выполнения плана нередко употребляют числовые сетки с 2-мя сопряженными шкалами. одна шкала охарактеризовывает выполнение плана в абсолютных величинах, иная — в относительных величинах (проценты выполнения плана). Числовые сетки употребляют для свойства выполнения планового задания за период динамики или в разрезе цехов и участков.
Построение графиков взаимосвязанных характеристик, один из которых равен произведению 2-ух остальных, можно производить при помощи так именуемых «символов Варзара». «3нак» строится вне системы прямоугольных координат в виде прямоугольника, основание которого пропорционально одному показателю — сомножителю, высота — другому.
При построении графиков (диаграмм) в системе прямоугольных координат нужно придерживаться последующих правил:
1. Любой график должен иметь заглавие, которое располагают под ним. В заглавии в короткой форме следует отразить содержание, пространство и время явления. Все графики нумеруются.
2. Оси координат должны быть названы и иметь единицы измерения.
3. На числовой оси следует откладывать лишь целые числа и в равном масштабе (к примеру: 20; 40; 60 и т.д., либо 1500; 3000; 4500 и т.д.). Заканчиваться числовая ось обязана той величиной, которая немногим больше наибольшей величины в начальной совокупы.
4. Если на одной числовой оси нужно расположить величины, относящиеся к одному и тому же явлению, но резко отличающиеся друг от друга по абсолютному значению, числовую ось можно порвать знаком (≈), что значит разрыв масштаба.
5. Если нужно отразить на одном графике (в одной системе прямоугольных координат) два-три явления, то вводят столько же доп числовых осей (осей ординат). Любая числовая ось обязана иметь свою размерность и собственный масштаб.
Тема 4. Абсолютные и относительные статистические величины
Под абсолютными величинами в статистике соображают характеристики, которые охарактеризовывают размеры (уровни, объемы) изучаемых экономических явлений.
Абсолютные величины являются начальной базой статистического анализа.
В отличие от абсолютных величин относительные величины являются величинами производными и рассчитываются на базе абсолютных.
В статистическом анализе употребляют последующие виды относительных величин: величины динамики, величины выполнения плана, величины структуры, величины координации, величины интенсивности, величины сопоставления.
При исследовании относительных величин динамики нужно, до этого всего, уяснить их роль в характеристике развития явления во времени. Следует направить внимание на нрав базы сопоставления (неизменная, переменная).
Приведем пример расчета относительных величин динамики (табл. 4.1).
Таблица 4.1
Выпуск товарной продукции на предприятии
Месяц
Тыс. руб.
Относительная величина динамики с неизменной базой сопоставления
Относительная величина динамики с переменной базой сопоставления
в коэффициентах
в процентах
в коэффициентах
в процентах
Январь
1390,7
1,000
100,0
–
–
Февраль
1426,9
1,026
102,6
1,026
102,6
Март
1492,6
1,073
107,3
1,046
104,6
Апрель
1547,5
1,113
111,3
1,037
103,7
Вычислим относительные величины динамики с неизменной базой сопоставления, приняв за базу январь: 1426,9 : 1390,7 = 1,026 ´ 100 = 102,6%; 1492,6 : 1390,7 = 1,073 ´ 100 = 107,3% и т.д.
Вычислим относительные величины динамики с переменной базой сопоставления, используя соотношения всякого следующего месяца к предшествующему: 1426,9 : 1390,7 = 1,026; 1492,6 : 1426,9 = 1,046 ´ 100 = 104,6% и т.д.
При вычислении относительных величин структуры следует уяснить их связь с группировкой статистических данных.
Приведем пример расчета (табл. 4.2).
Таблица 4.2
Распределение рабочих по тарифным разрядам
Тарифный разряд
Число рабочих в цехе
человек
в процентах к итогу
1
3
1,5
2
12
6,1
3
63
32,0
4
68
34,5
5
34
17,3
6
17
8,6
Итого:
197
100,0
Для свойства структуры рабочих по тарифным разрядам (в процентах) определяют удельный вес численности рабочих по подходящим разрядам в общей численности рабочих. Так, удельный вес численности рабочих 1 разряда составляет (3 : 197) ´ 100 = 1,5% и т.д. (см. табл. 4.2).
При вычислении относительных величин координации за базу сопоставления принимается какая-либо одна часть изучаемого явления, а другие части соотносятся с ней.
Для примера воспользуемся данными табл. 4.2. Если взять за базу сопоставления численность рабочих 2 разряда, тогда относительные величины координации составят: 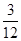 = 0,25;
= 0,25; 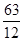 = 5,3;
= 5,3; 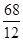 = 5,7;
= 5,7; 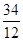 = 2,8;
= 2,8; 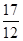 = 1,4, т.е. на всякого рабочего 2 разряда приходится в 4 раза меньше рабочих 1 разряда, 5 рабочих 3 разряда; 6 рабочих 4 разряда и т.д.
= 1,4, т.е. на всякого рабочего 2 разряда приходится в 4 раза меньше рабочих 1 разряда, 5 рабочих 3 разряда; 6 рабочих 4 разряда и т.д.
При вычислении относительных величин интенсивности нужно держать в голове, что они являются именованными показателями: так, коэффициент фондоотдачи указывает, какой размер продукции приходится на единицу цены главных производственных фондов; показатель производительности труда охарактеризовывает величину размера продукции в расчете на единицу трудовых издержек и т.д.
При вычислении относительных величин сопоставления необходимо уяснить, что сопоставлению меж собой подвергаются одноименные величины, относящиеся к различным объектам, взятые, как правило, за один и этот же период времени. К примеру, соотношение выпуска продукции на 2-ух предприятиях в отчетном периоде составило 102%.
Тема 5. Средние величины
Средние величины в статистике делают роль обобщающих характеристик, характеризующих изучаемую совокупа единиц по какому-либо признаку.
В статистике употребляют разные виды средних величин: средняя арифметическая обычная, средняя арифметическая взвешенная; средняя гармоническая, средняя геометрическая; структурные средние — мода и медиана.
При исследовании данной темы особенное внимание следует направить на то, что любой вид средней величины определяется зависимо от определенного экономического условия и от поставленной задачки. В неприятном случае средняя величина даст неверный итог и будет являться искаженной чертой изучаемой статистической совокупы.
Средняя величина рассчитывается по отменно однородной совокупы, значения которой приблизительно 1-го порядка.
Это — основное условие внедрения средней.
недозволено забывать о том, что средние величины в статистике являются величинами именованными и выражаются в тех же единицах, в каких выражен признак.
Нужно также уяснить значение средних моды и медианы, при помощи которых изучают структуру исследуемой совокупы.
Проиллюстрируем на определенных примерах порядок расчета всякого вида средних величин.
1. Распределение рабочих-наладчиков участка 1-го из цехов промышленного компании по стажу работы и квалификационным разрядам характеризуется последующими данными:
Таблица 5.1
Данные о составе рабочих
Стаж работы, лет
Число рабочих, чел.
Всего
в том числе имеющих разряд
4
5
6
До 10
9
2
4
3
10-20
7
–
2
5
20-30
3
–
1
2
30-40
2
–
–
2
Найти: а) средний разряд рабочих каждой возрастной группы; б) средний стаж рабочих участка.
Решение:
а) Для нахождения среднего разряда рабочих каждой возрастной группы следует применить среднюю арифметическую взвешенную:
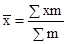 ;
;
в качестве веса (m) выступает определенный разряд рабочих. Так, для рабочих со стажем работы до 10 лет средний тарифный разряд составит:
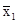 =
= 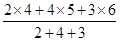 =
= 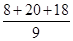 = 5 разряд.
= 5 разряд.
И так дальше по остальным возрастным группам.
б) Для нахождения среднего стажа рабочих на участке используют ту же среднюю арифметическую взвешенную, но уже для интервального ряда распределения.
При этом, в качестве «x» будут срединные значения признака в группах, а в качестве веса (m) принимают численность рабочих соответственной группы:
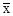 =
= 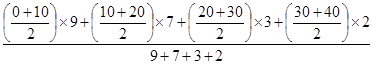 =
= 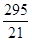 = 14 лет.
= 14 лет.
2. По последующим данным распределения рабочих цеха по проценту выполнения месячного задания найти моду и медиану.
Таблица 5.2
Данные о выполнении производственного задания
Выполнение месячного задания, процент
Число рабочих, чел.
Скопленные частоты от начала ряд
95-100
3
3
100-105
20
23
105-110
10
33
110-115
5
38
115-120
4
42
Итого
42
–
Модой в статистике именуют более нередко встречающееся в исследуемой совокупы
Моду определяют по формуле:
Mo = x0
+ 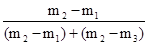 ∙ (x1
∙ (x1
– x0
),
где x0
и x1
— соответственно нижняя и верхняя границы модального интервала;
m2
— частота модального интервала;
m1
и m3
— частоты интервала, соответственно, предшествующего и последующего за модальным.
Подставим значения в формулу:
Mo = 100 + 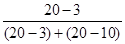 ´ (105 – 100) = 103,1%.
´ (105 – 100) = 103,1%.
По другому говоря, наибольшее число рабочих делают месячное задание на 103,1%.
Медианой в статистике именуют срединное задачки 42 : 2 = 21.
В нашей задачке медиана находится в интервале от 100 до 105% , потому что на данный интервал приходится скопленная частота 23.
Медиану определяют по формуле:
Me = x0
+ 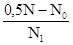 ∙ (x1
∙ (x1
– x0
),
где x0
и x1
— соответственно нижняя и верхняя границы медианного интервала;
N — сумма частот ряда;
N0
— сумма частот, накопившаяся до начала медианного интервала;
N1
— частота медианного интервала.
Подставим соответственное
Me = 100 + 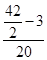 ´ 5 = 104,5%.
´ 5 = 104,5%.
Таковым образом, 50% всех рабочих делают производственное задание наименее чем на 104,5%; 50% — наиболее чем на 104,5%.
Тема 6. Ряды динамики
Рядами динамики именуют ряды, которые охарактеризовывают изменение явления во времени. Ряды динамики бывают моментные и интервальные. Моментные ряды охарактеризовывают изменение явления в динамике на определенный момент времени (почаще — на начало либо конец периода). Интервальные ряды охарактеризовывают изменение явления в динамике за определенный период времени (месяц, квартал, год).
В экономическом анализе употребляют аналитические характеристики динамики. К ним относят абсолютный прирост, средний абсолютный прирост, темп роста, темп прироста, средний темп роста, абсолютное
Разглядим на примере расчет аналитических характеристик ряда динамики (табл. 6.1).
Таблица 6.1
Данные о производстве в цехе
Месяц
Выпуск цехом товарной продукции, тыс. руб.
характеристики динамики
Абсолютный прирост (D), тыс. руб.
Темп роста (Тр
)
Темп прироста (Тпр
)
Абсолютное Абсолютный прирост (D) определяется как разность меж отчетным и предшествующим уровнями ряда динамики, т.е. по формуле:
D = yi
– yi
–1
,
где yi
, yi
–1
— уровни ряда динамики.
Так, к примеру, абсолютный прирост продукции цеха в феврале по сопоставлению c январем составил: 244 – 236 = 8 тыс. руб., а в марте по сопоставлению с февралем: 246 – 244 = 2 тыс. руб. и т.д.
Средний абсолютный прирост (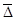 ) определяется на базе данных абсолютных приростов по последующей формуле:
) определяется на базе данных абсолютных приростов по последующей формуле:
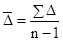 либо
либо 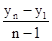 ,
,
где n — число уровней ряда динамики;
y1
и yn
— соответственно 1-ый и крайний уровни ряда динамики.
Темп роста (Тр
) определяется по формуле:
Тр
= 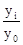 ´ 100%,
´ 100%,
где y0
— уровень ряда динамики, взятый за базу сопоставления.
Темп роста рассчитывается по принципу цепных и базовых соотношений. В том числе, когда за базу сопоставления принимается предшествующий период — это цепные характеристики темпа роста, когда сопоставление осуществляется с хоть каким остальным уровнем ряда динамики, взятым за базу сопоставления — базовые темпы роста.
Так, в феврале по сопоставлению с январем выпуск продукции в цехе составил: Тр2
= (244 : 236) ´ 100% = 103,4%, а в марте по сопоставлению с февралем: Тр3
= (246 : 244) ´ 100% = 100,8% и т.д.
Если за базу сопоставления взять январь, то выпуск продукции в цехе в марте по сопоставлению с январем составил: (246 : 236) ´ 100% = 104,2%, а в апреле по сопоставлению с январем: (249 : 236) ´ 100% = 105,5% и т.д.
Темп прироста (Тпр
) в отличие от темпа роста охарактеризовывает относительный прирост явления в отчетном периоде по сопоставлению с тем уровнем, с которым осуществляется сопоставление и определяется:
Тпр
= Тр
– 100.
Так, в марте размер продукции цеха по сопоставлению с февралем возрос на 0,8% (100,8 – 100), а по схватке с январем — на 4,2% (104,2 – 100) и т.д.
Абсолютное 1-го процента прироста и определяется по формуле:
А = 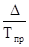 .
.
Так, в марте абсолютное
Средний темп роста (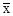 ) за период динамики определяют по формуле средней геометрической двойственным методом — на базе данных цепных коэффициентов динамики, или на базе данных абсолютных уровней ряда динамики по формуле:
) за период динамики определяют по формуле средней геометрической двойственным методом — на базе данных цепных коэффициентов динамики, или на базе данных абсолютных уровней ряда динамики по формуле:
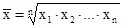 ∙100
∙100
либо
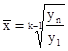 ∙100,
∙100,
где x1
, x2
, …, xn
— коэффициенты динамики по отношению к предшествующему периоду;
n — число коэффициентов динамики;
k — число абсолютных уровней ряда динамики.
Так, за 1-ое полугодие средний годичный темп роста продукции в цехе составил: 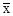 =
= 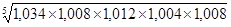 =
= 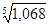 = 1,014 ´ 100 = 101,4% либо
= 1,014 ´ 100 = 101,4% либо 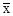 =
= 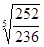 =
= 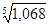 = 1,014 ´ 100 = 101,4%.
= 1,014 ´ 100 = 101,4%.
один из важных вопросцев, возникающих при исследовании рядов динамики — это выявление тенденции развития экономической закономерности в динамике. Для данной нам цели используются различные статистические способы, а именно, способ укрупнения интервалов, способ скользящей средней, способ аналитического сглаживания.
Более обычным в использовании является способ укрупнения интервалов, основанный на укрупнении периодов времени, к которым относятся уровни ряда. Выявление тенденции осуществляется по новенькому укрупненному ряду динамики.
иной способ — способ скользящей средней заключается в подмене начальных уровней ряда динамики средними арифметическими, отысканными по способу скольжения, начиная с первого уровня ряда с постепенным включением следующих уровней.
Более совершенным способом выявления тенденции ряда динамики является способ аналитического сглаживания, который заключается в подмене начальных уровней ряда новенькими, отысканными во времени «t» построением аналитического уравнения связи.
Разглядим на примере способности внедрения всякого из способов сглаживания при выявлении тенденции ряда динамики.
Известны последующие данные выполнения программки участком «молдинги» цеха ЗИЛ-130 прессового корпуса за 1989 г. (табл.6.2).
Таблица 6.2
Месяц
Выполнение программки, млн. руб.
t
t2
ty
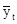 = 18,6 + 0,09t
= 18,6 + 0,09t
I
18,6
-6
36
-111,6
18,1
II
17,3
-5
25
-86,5
18,2
III
18,9
-4
16
-75,6
18,3
IV
18,2
-3
9
-54,6
18,3
V
17,9
-2
4
-35,8
18,4
VI
19,1
-1
1
-19,1
18,5
VII
19,6
1
1
19,6
19,2
VIII
17,5
2
4
35,0
19,1
IX
19,2
3
9
57,6
19,0
X
19,8
4
16
79,2
18,9
XI
18,3
5
25
91,5
18,8
XII
19,4
6
36
116,4
18,7
Итого:
223,8
0
182
16,1
223,5
1. По способу укрупнения интервалов имеем новейшие укрупненные поквартально уровни ряда динамики:
у1
= 18,6 + 17,3 + 18,9 = 54,8;
y2
= 18,2 + 17,9 + 19,1 = 55,2 и т.д.
Выровненный ряд динамики воспримет вид: 54,8 55,2 56,3 57,5.
Другими словами наблюдается четно выраженная тенденция роста выпуска молдингов цехом за 1989 г.
2. Употребляя те же данные, применим способ скользящей средней, используя семичленную скользящую среднюю. Тогда:
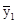 =
= 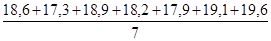 = 18,5;
= 18,5;
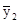 =
= 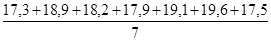 = 18,4 и т.д.
= 18,4 и т.д.
Выравненный при помощи семичленной скользящей средней ряд динамики воспримет вид: 18,5 18,4 18,6 18,7 18,8 19,0.
Таковым образом, подтверждается тенденция роста выпуска молдингов в течение 1989 г.
3. Используя способ отсчета от условного нуля введем условное обозначение времени «t», придав ему определенные значения так, чтоб ∑t = 0 (см. табл. 6.2).
Судя по выявленной при помощи 2-ух прошлых способов тенденции выпуска молдингов в течение года, можно сказать, что более возможна линейная зависимость данного распределения от времени «t» и данному распределению соответствует уравнение прямой 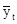 = a0
= a0
+ a1
t.
Для нахождения характеристик a0
и a1
используем систему уравнений
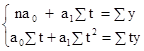 ,
,
потому что ∑t = 0, о имеем
a0
= 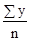 =
= 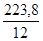 = 18,6;
= 18,6;
a1
= 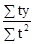 =
= 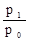 = 0,09.
= 0,09.
Как следует, уравнение прямой воспримет вид:
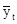 = 18,6 + 0,09t и будет в данном случае разыскиваемым, потому что ∑y = ∑
= 18,6 + 0,09t и будет в данном случае разыскиваемым, потому что ∑y = ∑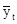 .
.
Тема 7. характеристики варианты
Наряду со средней величиной, характеризующей обычный уровень варьирующего признака, около которого колеблются отдельные значения признака, разглядывают характеристики варианты (колеблемости) признака, дозволяющие количественно измерить величину данной нам колеблемости.
К показателям варианты относят: размах варианты, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент варианты.
Простым показателем варианты является размах варианты, который рассчитывается по последующей формуле:
R = Xmax – Xmin,
где Xmax, Xmin — соответственно, наибольшее и малое значения признака в исследуемой совокупы.
Размах варианты охарактеризовывает спектр колебаний признака в изучаемой совокупы и измеряется в тех же единицах, в каких выражен признак.
Рассчитывают среднее линейное отклонение, которое бывает невзвешенное и взвешенное. Если каждое
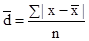 ,
,
где x —
n — количество вариант.
Если имеется некая повторяемость значений признака, то применяется формула среднего линейного отличия взвешенного:
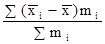 ,
,
где m — частота.
Среднее линейное отклонение охарактеризовывает абсолютный размер колеблемости признака около средней и измеряется в тех же единицах, в каких выражен признак.
Более четким показателем варианты является среднее квадратическое отклонение. Для его определения за ранее рассчитывают показатель дисперсии. Дисперсия невзвешенная определяется по формуле:
σ2
=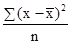 .
.
Дисперсия взвешенная определяется по формуле:
σ2
=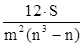 .
.
Тогда, соответственно, для расчета среднего квадратического отличия невзвешенного употребляют формулу:
σ =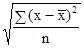 ,
,
а для расчета среднего квадратического отличия взвешенного — последующую формулу:
σ =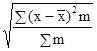 .
.
Как и среднее линейное отклонение, среднее квадратическое отклонение охарактеризовывает абсолютный размер колеблемости признака около средней, но является наиболее четкой чертой.
В отличие от среднего линейного и среднего квадратического отличия коэффициент варианты является мерой относительной колеблемости признака около средней и охарактеризовывает степень однородности признака в изучаемой совокупы. Он определяется по формуле:
υσ
= 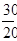 ´ 100%.
´ 100%.
Если исследуемую совокупа единиц расчленить на группы, то вправе считать, что общая дисперсия всей совокупы варьирует (меняется) под воздействием дисперсий для каждой отдельной группы, так именуемых групповых либо личных дисперсий и межгрупповой дисперсии. Эти дисперсии соединены меж собой правилом сложения дисперсий. При использовании правила сложения дисперсий в экономическом анализе по величине личной дисперсии может решаться задачка выявления более действенной в производстве системы (формы, структуры и т.п.) организации труда, его оплаты и т.п.
Личные либо групповые дисперсии охарактеризовывают колеблемость изучаемого признака в каждой отдельной группе и определяются по последующей формуле:
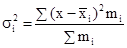
и их средняя величина
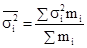 ,
,
где i = 1, 2, …, n — номер группы;
mi
— численность единиц в группе.
Межгрупповая дисперсия охарактеризовывает колеблемость личных средних около общей средней 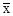 и определяется последующим образом:
и определяется последующим образом:
γ2
=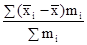 .
.
При соблюдении правила сложения дисперсий обязано соблюдаться равенство:
σ2
= 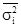 + γ2
+ γ2
.
Проиллюстрируем расчет характеристик варианты по данным о распределении рабочих по стажу работы (табл. 7.1).
1. R = Xmax – Xmin = 14 – 10 = 4 года, т.е. спектр колебания стажа рабочих в исследуемой совокупы составляет 4 года.
2. 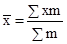 =
= 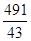 = 11,4 года
= 11,4 года
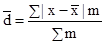 =
= 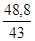 = 1,1 года.
= 1,1 года.
Таблице 7.1
Стаж работы рабочих
Стаж работы рабочего, лет (x)
Число рабочих, чел. (m)
x∙m
x –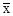
| x –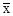 |m
|m
(x –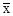 )2
)2
(x –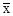 )2
)2
m
10
14
140
-1,4
19,6
1,96
27,44
11
11
121
-0,4
4,4
0,16
1,76
12
8
96
0,6
4,8
0,36
2,88
13
6
78
1,6
9,6
2,56
15,36
14
4
56
2,6
10,4
6,76
24,04
Итого
43
491
–
48,8
11,80
74,48
В среднем на 1,1 года отклоняется стаж отдельных рабочих от среднего стажа по совокупы.
3. σ2
=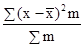 =
= 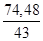 = 1,73;
= 1,73;
σ =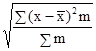 =
= 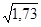 = 1,3 года.
= 1,3 года.
Величина σ = 1,3 года охарактеризовывает колеблемость стажа работы рабочих в данной совокупы:
υσ
= 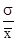 ´ 100 =
´ 100 = 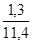 ´ 100 = 11,4%.
´ 100 = 11,4%.
Таковым образом, на 11,4% варьирует состав рабочих по стажу работы в исследуемой совокупы.
Тема 8. Индексы
В статистике индексами именуют относительные величины, показывающие соотношение характеристик во времени, пространстве, также фактических характеристик с плановыми.
Индексы измеряются в процентах.
Для неких обычных, единичных явлений, которые допускают конкретное сопоставление, строят личные индексы. денька явлений сложных, состоящих из конкретно несоизмеримых частей, строят сводные индексы. Так, для свойства динамики производства определенного вида продукции, применяется личный индекс. Если же исследователя интересует динамика выпуска всей продукции компании, то в этом случае строится сводный индекс, потому что отдельные виды продукции компании конкретно несоизмеримы.
Разработанная статистикой теория индексов дозволяет решить последующие задачки:
1) определять соотношение характеристик во времени, пространстве, фактических данных с плановыми;
2) выявлять абсолютные результаты измерения характеристик в подобных направлениях;
3) определять относительное и абсолютное воздействие отдельных причин на такое изменение при условии, что причины представлены в виде произведения.
В теории индексов более нередко употребляются последующие обозначения: I — личный индекс; J — сводный индекс.
порядок построения личных индексов очень прост: в числителе дроби записывается показатель на уровне отчетного периода, в знаменателе — на уровне базового периода. к примеру:
Ip
= 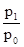 ; It
; It
= 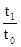 ; Iq
; Iq
= 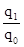 и т.д.,
и т.д.,
где Ip
— личный индекс цен;
It
— личный индекс трудозатратности;
Iq
— личный индекс продукции;
p1
и p0
— стоимость единицы продукции, соответственно, в отчетном и базовом периодах, руб.;
t1
и t0
— трудозатратность производства единицы продукции, соответственно, в отчетном и базовом периодах, ч;
q1
и q0
— количество произведенной продукции, соответственно, в отчетном и базовом периодах, шт.
Есть цепные и базовые личные индексы. В цепных индексах любой следующий период сравнивается с предшествующим, к примеру:
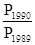 ;
; 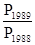 ;
; 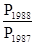 и т.д.
и т.д.
Несложно увидеть, что перемножение цепных индексов дает в итоге сопоставление явлений, разбитых промежутков времени (базовые индексы):
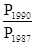 =
= 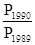 ´
´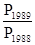 ´
´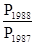 .
.
естественно, если в задачке известен базовый индекс и какие-то из цепных, то для нахождения остальных цепных индексов нужно создавать деление.
Следует знать, что индексы динамики, планового задания и выполнения плана соединены меж собой известным из теории относительных величин соотношением:
Iдинамики = Iпл. задания ´Iвыполнения плана.
Если в задачке требуется отыскать абсолютное изменение какого-то явления, то оно определяется как разница меж числителем и знаменателем индекса:
(p1
– p0
); (t1
– t0
) и т.д.
Если при всем этом ставится задачка найти, как влияет это изменение на некое многофакторное явление, то отысканная разность меж числителем и знаменателем высококачественного индекса (цен, трудозатратности и т.п.) множится на соответственный количественный фактор (количество продукции, численность работающих и т.п.) на уровне отчетного периода. Разность меж числителем и знаменателем количественного индекса (продукции, численности работающих и т.п.) множится на соответственный высококачественный фактор (трудозатратность и т.п.) на уровне базового периода:
(p1
– p0
)q1
— размер экономии (перерасхода) валютных средств от понижения (увеличения) цен;
(t1
– t0
)q1
— размер роста (уменьшения) издержек труда на Создание продукции от увеличения (понижения) трудозатратности;
(q1
– q0
)p0
— размер экономии (перерасхода) валютных средств от конфигурации размера выпуска продукции;
(q1
– q0
)t0
— размер роста (уменьшения) издержек труда на Создание продукции от конфигурации размера выпуска продукции и т.д.
В отличие от личных индексов, сводные индексы представляют собой итог сопоставления сложных явлений, состоящих из конкретно несоизмеримых частей.
Сводные индексы представляют собой соотношение сумм произведений индексируемых величин и их соизмерителей. В качестве соизмерителей могут выступать: трудозатратность производства продукции (t), стоимость единицы продукции (p), себестоимость единицы продукции (z). Заглавие сводного индекса определяется изменяющимся (индексируемым) показателем. Индексируемый показатель записывают в числителе на уровне отчетного периода, в знаменателе — на уровне базового периода либо на уровне планового задания. Если индексируется высококачественный показатель (стоимость, трудозатратность, себестоимость), то соответственный ему количественный соизмеритель фиксируется на уровне отчетного периода. Если индексируется количественный показатель, то соответственный ему высококачественный соизмеритель фиксируется на уровне базового периода либо на уровне планового задания. Исходя из этого, сводный индекс цен запишется:
Jp
=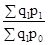 ;
;
сводный индекс трудозатратности: Jt
=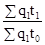 ;
;
сводный индекс себестоимости: Jz
=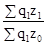 ;
;
сводный индекс физического размера продукции:
Jq
=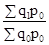 (при наличии соизмерителя p);
(при наличии соизмерителя p);
Jq
=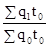 (при наличии соизмерителя t);
(при наличии соизмерителя t);
Jq
=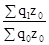 (при наличии соизмерителя z).
(при наличии соизмерителя z).
Индексы цен, трудозатратности и себестоимости продукции относятся к индексам неизменного состава, потому что q = const. Индексы физического размера продукции независимо от соизмерителя относятся к индексам структурных сдвигов, потому что учитывается изменение в ассортименте и объеме продукции. В том случае, когда в сводном индексе индексируется сам показатель и его соизмеритель, оба составляющих в числителе записываются на уровне отчетного периода, в знаменателе — на уровне базового периода, а заглавие сводного индекса определяется индексируемыми составляющими. Так, сводный индекс размера продукции в стоимостном выражении запишется Jqp
=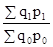 ; индекс издержек труда на Создание продукции Jqt
; индекс издержек труда на Создание продукции Jqt
=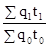 ; индекс валютных издержек на Создание продукции Jqz
; индекс валютных издержек на Создание продукции Jqz
=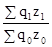 .
.
Такие индексы относятся к индексам переменного состава, потому что варьируют оба составляющих.
В статистическом анализе употребляется связь индексов переменного состава и структурных сдвигов, которая проявляется в виде 2-ух параметров индексов.
1-ое свойство индексов: индекс переменного состава равен произведению индексов неизменного состава и структурных сдвигов:
Jqp
= Jq
∙ Jp
; 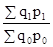 =
= 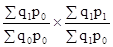 ;
;
Jqt
= Jq
∙ Jt
; 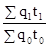 =
= 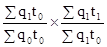 ;
;
Jqz
= Jq
∙ Jz
; 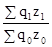 =
= 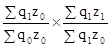 .
.
2-ое свойство индексов: разность числителя и знаменателя индекса переменного состава равна сумме разностей числителя и знаменателя индексов неизменного состава и структурных сдвигов:
Dqp(
qp
)
= Dqp(
q
)
+ Dqp(
p
)
; ∑q1
p1
– ∑q0
p0
= (∑q1
p0
– ∑q0
p0
) + (∑q1
p1
– ∑q1
p0
);
Dqt(
qt
)
= Dqt(
q
)
+ Dqt(
t
)
; ∑q1
t1
– ∑q0
t0
= (∑q1
t0
– ∑q0
t0
) + (∑q1
t1
– ∑q1
t0
);
Dqz(
qz
)
= Dqz(
q
)
+ Dqz(
z
)
; ∑q1
z1
– ∑q0
z0
= (∑q1
z0
– ∑q0
z0
) + (∑q1
z1
– ∑q1
z0
).
Разглядим пример:
По одному из подразделений промышленного компании известны последующие данные (табл. 8.1).
Таблица 8.1
Вид продукции
количество произведенной продукции, тыс. шт.
Стоимость 1 шт., руб.
Базовый период
Отчетный период
Базовый период
Отчетный период
А
15
20
0,8
0,7
Б
1,5
2
2,0
1,5
В
5
10
1,0
0,8
Рассчитаем личные индексы продукции и личные индексы цен.
Личные индексы по подходящим видам продукции составят:
Iq
(А)
= 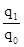 =
= 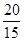 ´ 100 = 133,3%;
´ 100 = 133,3%;
Iq
(Б)
= 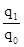 =
= 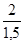 ´ 100 = 133,3%;
´ 100 = 133,3%;
Iq
(В)
= 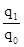 =
= 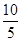 ´ 100 = 200%.
´ 100 = 200%.
Другими словами в отчетном периоде по сопоставлению с базовым произведено продукции вида «А» и «Б», соответственно, на 33,3% больше, а вида «В» — на 100% больше.
Личные индексы цен по подходящим видам продукции составят:
Ip
(А)
= 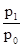 =
= 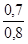 ´ 100 = 87,5%;
´ 100 = 87,5%;
Ip
(Б)
= 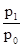 =
= 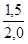 ´ 100 = 75,0%;
´ 100 = 75,0%;
Ip
(В)
= 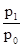 =
= 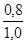 ´ 100 = 80,0%.
´ 100 = 80,0%.
Другими словами стоимость единицы продукции вида «А» в отчетном периоде по сопоставлению с базовым снизилась на 12,5% (100 – 87,5), вида «Б» — на 25% (100 – 75) и вида «В» — на 20% (100 – 80).
Личные индексы определенного вида продукции в стоимостном выражении, соответственно, составят:
Ip
(А)
= 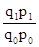 =
= 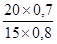 ´ 100 =
´ 100 = 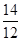 ´ 100 = 116,7%;
´ 100 = 116,7%;
Ip
(Б)
= 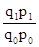 =
= 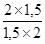 ´ 100 =
´ 100 = 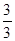 ´ 100 = 100%;
´ 100 = 100%;
Ip
(В)
= 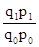 =
= 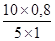 ´ 100 =
´ 100 = 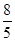 ´ 100 = 160%.
´ 100 = 160%.
Таковым образом, размер продукции в стоимостном выражении вида «А» в отчетном периоде по сопоставлению с базовым возрастет на 16,7% (116,7 – 100), вида «В» — на 60% (160 – 100) и вида «Б» — остается без конфигурации (100 – 100).
Для того, чтоб ответить на вопросец, как уменьшился размер всей продукции компании в отчетном периоде по сопоставлению с базовым, нужно высчитать сводные индексы продукции, цен и физического размера продукции.
Сводный индекс размера продукции в стоимостном выражении составит:
Jqp
= 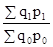 =
= 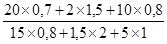 ´ 100 =
´ 100 = 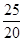 ´ 100 = 125%;
´ 100 = 125%;
Сводный индекс цен составит:
Jp
= 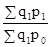 =
=  ´ 100 =
´ 100 = 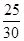 ´ 100 = 83,3%;
´ 100 = 83,3%;
Сводный индекс физического размера продукции составит:
Jq
= 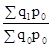 =
= 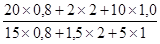 ´ 100 =
´ 100 = 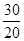 ´ 100 = 150%.
´ 100 = 150%.
Используя 1-ое свойство индексов, имеем:
Jqp
= Jq
∙ Jp
; 125% = 1,5 ´ 0,833 ´ 100%.
Используя 2-ое свойство индексов, имеем:
Dqp(
qp
)
= Dqp(
q
)
+ Dqp(
p
)
, т.е. (25 – 20) = (30 – 20) + (25 – 30) либо (+5) = (+10) + (-5).
Таковым образом, можно прийти к выводу: объём продукции в стоимостном выражении возрос в целом на 25%, либо на 5´(25 – 20) тыс. руб., в том числе за счет понижения цен на 16,7% (83,3 – 100) размер снизился на 5 тыс. руб. (25 – 30), а за счет роста физического размера продукции на 50% (150 – 100) размер продукции в стоимостном выражении возрос на 10 тыс. руб.
Тема 9. Связи явлений
1-ый шаг исследования связи явлений — выделение главных причинно-следственных связей и отделение их от второстепенных. 2-ой шаг — построение модели. Крайний шаг — интерпретация результатов.
признаки-аргументы именуются факторами, а признаки-функции — плодами (действенными признаками).
Связи меж явлениями делят по степени тесноты связи (полная либо многофункциональная связь, неполная либо статистическая связь), по направлению (ровная, оборотная), по аналитическому выражению (линейная, нелинейная).
Для выявления связи, ее нрава, направления употребляют способы приведения параллельных данных, балансовый, аналитических группировок, графический. Сущность способа приведения параллельных данных: приводят два ряда данных о 2-ух признаках, связь меж которыми желают выявить, и по способ заключается в построении балансов — таблиц, где результат одной части равен итогу иной.
Способы аналитических группировок и графический изложены в соответственных темах.
Комфортная форма изложения данных — корреляционная таблица (табл. 9.1).
Таблица 9.1
Корреляционная таблица
Часовая выработка ткани , м
количество станков, обслуживаемых одной работницей, шт.
5-7
7-9
9-11
11-13
13-15
15-17
17-19
Итого
10 — 15
7
4
2
1
14
15 — 20
3
8
5
4
20
20 — 25
2
11
8
2
23
25 — 30
5
13
7
1
26
30 — 35
1
16
3
20
35 — 40
2
6
19
3
30
40 — 45
3
7
18
28
Итого:
10
14
21
30
33
32
21
161
Таблица указывает, что частоты концентрируются у диагонали, идущей из левого верхнего угла в правый нижний. Это показывает на то, что связь меж количеством обслуживаемых работницей станков и ее часовой выработкой ткани ровная (с повышением числа обслуживаемых станков возрастает выработка) либо близкая к прямой (концентрация частот идет практически по прямой полосы).
По данным таблицы можно высчитать среднюю выработку по каждой из 7 групп работниц, выделенных по числу обслуживаемых станков. Обозначив эти средние значения через 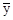 и произведя расчеты, получаем:
и произведя расчеты, получаем: 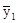 = 14,0;
= 14,0; 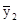 = 16,79;
= 16,79; 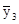 = 22,51;
= 22,51; 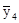 = 24,67;
= 24,67; 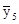 = 32,65;
= 32,65; 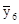 = 36,88;
= 36,88; 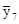 = 41,79.
= 41,79.
Данные таблицы и результаты расчетов можно изобразить графически при помощи поля корреляции. Ломаная линия на графике (линия значений 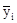 ) именуется эмпирической линией регрессии.
) именуется эмпирической линией регрессии.
характеристики тесноты связи. Для оценки тесноты связи применяется ряд характеристик, одни из которых именуются эмпирическими либо непараметрическими, остальные (выводимые строго математически) — теоретическими.
Коэффициент символов (коэффициент Фехнера) рассчитывается на основании определения символов отклонений вариантов 2-ух взаимосвязанных признаков от их средних величин.
Если число совпадений символов обозначать через a, число несовпадений — через b, а сам коэффициент — через i , то можно записать формулу этого коэффициента так:
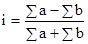 .
.
Коэффициент корреляции рангов (коэффициент Спирмена) рассчитывается не по значениям 2-ух взаимосвязанных признаков, а по их рангам последующим образом:
ρx/y
= 1 – 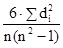 ,
,
где di
— разности рангов; n — число пар рангов.
Для определения тесноты связи меж 3-мя и наиболее признаками применяется ранговый коэффициент согласия — коэффициент конкордации, который рассчитывается по формуле:
w = 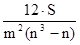 ,
,
где m — количество причин;
n — число наблюдений;
S — сумма квадратов отклонений рангов.
Величина коэффициента конкордации наиболее 0,5 указывает, что меж исследуемыми величинами имеется тесноватая зависимость.
Если при определении тесноты связи при помощи приведенных ранговых коэффициентов имеются связные ранги, т.е. если двум либо наиболее показателям присвоен один и этот же ранг, то расчеты проводятся по формулам:
коэффициент Спирмена: ρx/y
= 1 – 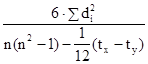 ;
;
коэффициент конкордации: w = 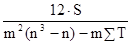 ,
,
где T = 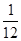 (t3
(t3
– t), а t — количество связных рангов по отдельным показателям.
При исследовании соц явлений и действий огромное
a
b
a+b
c
d
c + d
a + c
b + d
a + b + c + d
Для определения тесноты связи 2-ух высококачественных признаков, любой из которых состоит лишь из 2-ух групп, используются коэффициенты ассоциации и контингенции. Для их вычисления строится таблица, которая указывает связь меж 2-мя явлениями, каждое из которых обязано быть другим, т.е. состоящим из 2-ух отменно хороших друг от друга значений признака (к примеру, неплохой, нехороший).
Коэффициенты рассчитываются по формулам:
A = 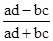 — ассоциации;
— ассоциации;
K = 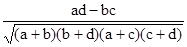 — контингенции.
— контингенции.
Коэффициент контингенции постоянно меньше коэффициента ассоциации. Связь считается подтвержденной, если A ³ 0,5, либо K³ 0,3.
Если любой из высококачественных признаков состоит наиболее чем из 2-ух групп, то для определения тесноты связи может быть применение коэффициента обоюдной сопряженности Пирсона. Этот коэффициент рассчитывается по формуле:
C = 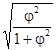 ,
,
где j2
— показатель обоюдной сопряженности.
Расчет коэффициента обоюдной сопряженности проводится по последующей схеме:
Группа признака A
Группа признака В
Итого
B1
B2
B3
A1
f1
f2
f3
n1
A2
f4
f5
f6
n2
A3
f7
f8
f9
n3
m1
m2
m3
Расчетj2
проводится так:
по первой строке 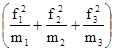 : n1
: n1
= L1
;
по 2-ой строке 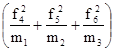 : n2
: n2
= L2
;
по третьей строке 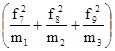 : n3
: n3
= L3
;
Как следует, j2
= L1
+ L2
+ L3
– 1.
Интерпретация непараметрических коэффициентов связи в неких вариантах, в особенности когда они имеют отрицательное значения к единице, тем теснее связь меж исследуемыми признаками.
Корреляция и регрессияКлассические способы корреляционно-регрессионного анализа разрешают не только лишь оценить тесноту связи, да и выразить эту связь аналитически. Применению корреляционно-регрессионного анализа должен предшествовать высококачественный, теоретический анализ исследуемого социально-экономического явления либо процесса.
Связь меж 2-мя факторами аналитически выражается уравнениями:
прямой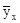 = a0
= a0
+ a1
x;
гиперболы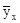 = a0
= a0
+ 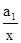 ;
;
параболы 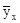 = a0
= a0
+ a1
x + a2
x2
(либо иной ее степени);
степенной функции 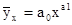 .
.
Параметр a0
указывает усредненное воздействие на действенный признак неучтенных (не выделенных для исследования) причин. Параметр a1
— коэффициент регрессии указывает, на сколько меняется в среднем значение действенного признака при увеличении факторного на единицу. На базе этого параметра рассчитываются коэффициенты эластичности, которые демонстрируют изменение действенного признака в процентах зависимо от конфигурации факторного признака на 1%:
Э = a1
∙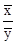 .
.
Для определения характеристик уравнений употребляется способ меньших квадратов, на основании которого строится соответственная система уравнений.
Теснота связи при линейной зависимости измеряется при помощи линейного коэффициента корреляции:
r = 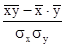 ,
,
а при криволинейной зависимости при помощи корреляционного дела:
h = 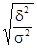 .
.
Расчет коэффициентов регрессии несколько осложняется, если ряды по исследуемым факторам сгруппированы, а связь криволинейная.
Если зависимость меж 2-мя факторами выражается уравнением гиперболы
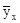 = a0
= a0
+ 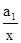 ,
,
то система уравнений для определения характеристик a0
и a1
такая:
na0
+ a1
∑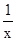 = ∑y;
= ∑y;
a0
∑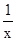 + a1
+ a1
∑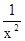 = ∑y
= ∑y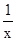 .
.
Для определения характеристик уравнения регрессии, выраженного степенной функцией 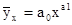 , приводят функцию к линейному виду: lg
, приводят функцию к линейному виду: lg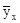 = lga0
= lga0
+ a1
lgx, отсюда система уравнений для определения характеристик запишется:
n∙lga0
+ a1
∑lgx = ∑lgy;
lga0
∑lgx + a1
∑(lgx)2
= ∑lgy∙lgx.
Зависимость меж 3-мя и наиболее факторами именуется множественной либо многофакторной корреляционной зависимостью. Линейная связь меж 3-мя факторами выражается уравнением:
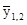 = a0
= a0
+ a1
x + a2
z,
а система обычных уравнений для определения неведомых характеристик a0
, a1
, a2
будет последующей:
na0
+ a1
∑x + a2
∑z = ∑y;
a0
∑x + a1
∑x2
+ a2
∑zx = ∑yx;
a0
∑z + a1
∑xz + a2
∑z2
= ∑yz.
Теснота связи меж 3-мя факторами измеряется при помощи множественного (совокупного) коэффициента корреляции:
R = 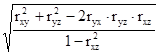 ,
,
где rij
— парные коэффициенты корреляции меж надлежащими факторами.
Для наиболее углубленного анализа рассчитываются личные коэффициенты корреляции.
Дисперсионный анализ связи. При маленьком числе наблюдений изучить воздействие 1-го либо нескольких факторных признаков на действенный можно, используя способы дисперсионного анализа. Дисперсионный анализ проводится расчетом дисперсий: общей, межгрупповой и внутригрупповой. Общую дисперсию именуют дисперсией комплекса, межгрупповую — факторной, внутригрупповую — остаточной.
Дисперсионный анализ заключается в сопоставлении факторной и остаточной дисперсий. Если различие меж ними значимо, то факторный признак, т.е. признак, положенный в основание группировки, оказывает существенное воздействие на действенный. При исследовании действия на действенный признак лишь 1-го факторного, т.е. однофакторного комплекса дисперсии рассчитываются:
дисперсия комплекса 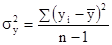 ;
;
факторная дисперсия 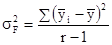 ;
;
остаточная дисперсия 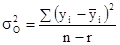 ,
,
где n – 1, r – 1, n – r — надлежащие числа степеней свободы;
r — число уровней (групп).
На основании дисперсий проводится расчет аспекта Фишера Fp
. Если расчетное
Тема 10. Выборочное наблюдение
Главными вопросцами теории выборочного наблюдения, требующими практического закрепления на базе решения задач и выполнения упражнений, являются:
— определение предела случайной ошибки репрезентативности для разных типов выборочных черт с учетом особенностей отбора;
— определение размера подборки, обеспечивающего нужную репрезентативность выборочной свойства, с учетом особенностей отбора.
Ошибка репрезентативности, либо разность меж выборочной и генеральной чертой (средней, толикой), возникающая в силу несплошного наблюдения, в базе которого лежит случайный отбор, рассчитывается как предел наивероятной ошибки. В качестве уровня гарантийной вероятности обычно берется 0,954 либо 0,997. Тогда предел ошибки определяется величиной двойной либо тройной средней ошибки подборки: D = 2m при P = 0,954; D = 3m при P = 0,997, либо в общем виде D = tm (t — коэффициент, связанный с вероятностью, гарантирующей итог).
Величина средней ошибки подборки различна для отдельных разновидностей случайного отбора. При более обычный системе — собственно-случайном повторном отборе — средняя ошибка определяется последующими формулами:
личный отбор:
m = 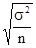 =
= 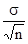 ,
,
где σ2
— общая дисперсия признака;
n — число отобранных единиц наблюдения;
групповой (гнездовой, серийный) отбор:
m = 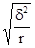 =
= 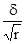 ,
,
где δ2
— межгрупповая дисперсия;
r — число отобранных групп (гнезд, серий) единиц наблюдения.
При практических расчетах ошибок репрезентативности нужно учесть последующее:
1. Заместо генеральной дисперсии употребляется соответственная выборочная дисперсия. Так, заместо общей дисперсии толики в генеральной совокупы берется общая дисперсия частости:
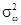 = w(1 – w) заместо
= w(1 – w) заместо 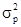 = pq.
= pq.
2. В случае бесповторного метода отбора (также механического) следует подразумевать поправки (K) к ошибке повторной подборки на бесповторность отбора:
K = 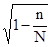 < 1 либо K =
< 1 либо K = 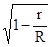 < 1.
< 1.
Разумеется, что воспользоваться данной нам поправкой целенаправлено только тогда, когда относительный размер подборки составляет приметную часть генеральной совокупы (не наименее 10%, тогда K £ 0,95).
3. При районированном отборе из типических групп единиц генеральной совокупы употребляется средняя из личных (групповых) дисперсий. Так, при личном отборе, пропорциональном размерам типических групп, имеем:
D = 2m = 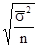 =
= 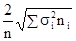 при P = 0,954,
при P = 0,954,
где 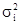 — личная дисперсия i-й группы;
— личная дисперсия i-й группы;
ni
— размер подборки в i-й группе.
Определение ошибок выборочных черт дозволяет установить наивероятные границы нахождения соответственных генеральных характеристик:
для средней: 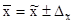 ,
,
где 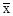 — генеральная средняя;
— генеральная средняя;
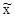 — выборочная средняя;
— выборочная средняя;
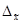 — ошибка выборочной средней;
— ошибка выборочной средней;
для толики: p = w±Dw,
где p — генеральная толика;
w — выборочная толика (частость);
Dw — ошибка выборочной толики.
Пример. С вероятностью 0,954 необходимо найти границы среднего веса пачки чая для всей партии, поступившей в торговую сеть, если контрольная выборочная проверка отдала последующие результаты (1-ые две графы табл. 10.1).
Таблица 10.1
Результаты взвешивания чая
Вес, г (x)
количество пачек (m)
Расчетные графы
x¢
m¢
x¢m¢
(x¢)2
m¢
48 — 49
20
-1
2
-2
2
49 — 50
50
0
5
0
0
50 — 51
20
+1
2
2
2
51 — 52
10
+2
1
2
4
Итого:
100
–
10
2
8
1. Средний вес пачки чая по выборке:
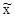 =
= 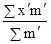 ´K + x0
´K + x0
= 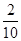 ´ 1 + 49,5 = 49,7 г.
´ 1 + 49,5 = 49,7 г.
2. Выборочная дисперсия веса пачки чая:
σ2
= 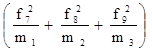 =
= 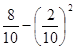 = 0,76.
= 0,76.
3. Средняя ошибка выборочной средней:
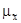 =
= 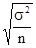 =
= 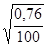 = 0,087 г.
= 0,087 г.
4. Предел для ошибки с вероятностью 0,954:
D = 2m = 0,174 г » 0,2 г.
5. Границы генеральной средней:
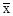 =
= 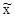 ±D = 49,7 ± 0,2 г.
±D = 49,7 ± 0,2 г.
Таковым образом, с вероятностью 0,954 можно утверждать, что вес пачки чая в среднем для всей партии не наиболее 49,9 г и не наименее 49,5 г.
Определение размера подборки при данной ее точности является неувязкой, оборотной рассмотренной нами — определению ошибки подборки при данном ее объеме. Формула размера подборки выходит из соответственной формулы предельной ошибки. Так, получаем для личного бесповторного отбора:
n =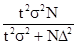 ;
;
группового бесповторного отбора:
r =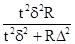 .
.
При решении задач на определение нужного размера подборки следует подразумевать, что заместо генеральной дисперсии определенного вида берется ее оценка — примерное
Пример. необходимо найти абсолютный и относительный объемы личного отбора для исследования генеральной толики, чтоб ошибка частости с вероятностью 0,954 не превосходила 0,02, если подборка делается из генеральной совокупы размера: а) 1000; б) 100000 единиц.
Используя формулу n =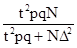 , в какой полагаем t = 2 (гарантийная возможность равна 0,954), а pq = 0,25, имеем:
, в какой полагаем t = 2 (гарантийная возможность равна 0,954), а pq = 0,25, имеем:
а) n = 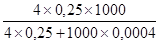 = 714, либо 71,4%;
= 714, либо 71,4%;
б) n = 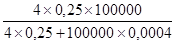 = 2439, либо 2,44%.
= 2439, либо 2,44%.
Тема 11. законы распределения
Конечной целью обработки инфы способами математической статистика, если идет речь о огромных подборках, является получение закона распределения исследуемой случайной величины. Это соединено с тем, что законраспределения является практически, тем аппаратом, который дозволяет найти возможность возникновения (либо, напротив, непоявления) случайной величины в тот либо другой период времени либо возможность того, что случайная величина попадет в тот либо другой интервал ее вероятных значении. Этот шаг статистической обработки является одним из более принципиальных, потому что ошибка при выбирании того либо другого закона распределения приводит к ошибкам при предстоящем решении практических задач.
Если проанализировать все этапы статистической обработки, то можно прийти к выводу, что влекущими за собой более значительные ошибки, а, как следует, более ответственными, являются этапы, на которых решаются последующие задачки:
1. Может быть ли объединение нескольких малых либо средних выборок в одну.
2. Отбрасывать либо учесть резко отличающиеся результаты.
3. Справедливо ли изготовленное предположение о законе распределения случайной величины.
Разглядим эти этапы наиболее тщательно.
1. Потому что для установления закона распределения нужны огромные подборки, то на практике нередко встает вопросец о объединении нескольких выборок, любая из которых мала для решения поставленной задачки и получения одной общей подборки, удовлетворяющей предъявленным к ней требованиям. Потому, что совершенно характерно для статистической обработки, хоть какое из некорректных решений (как положительное, так и отрицательное) по поводу объединения выборок приводит к ненужным результатам, либо к невозможности установить законраспределения, если подборки не соединяются воединыжды, либо к неверному выводу о нраве закона распределения.
Для решения данной нам задачки употребляют аспекты, при помощи которых с разной формулировкой практически дается ответ на один и этот же вопросец: принадлежат либо не принадлежат исследуемые подборки одной генеральной совокупы, другими словами автоматом решается задачка о способности либо невозможности их объединения. Как правило, все эти аспекты основаны на сопоставлении выборочных черт (выборочных дисперсий либо средних величин) меж собой либо с надлежащими генеральными чертами. Почти всегда внедрение этих критериев подразумевает обычный либо логарифмически-нормальный законраспределения для каждой подборки. При остальных же законах распределения эти аспекты неправильны и их внедрение может привести к неверным результатам.
Более применяемыми являются последующие аспекты:
а) аспекты, основанные на сопоставлении дисперсий: аспект 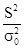 , аспект Фишера (F =
, аспект Фишера (F = 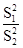 ), аспект Хартлея (Fmax
), аспект Хартлея (Fmax
= 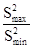 ), аспект Кочрена (Gmax
), аспект Кочрена (Gmax
= 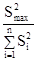 ), аспект Бартлета (χ2
), аспект Бартлета (χ2
);
б) аспекты, основанные на сопоставлениях средних величин: аспект Стьюдента (t), аспект Z и остальные.
Для всех критериев в качестве нулевой догадки (H0
) выдвигается предположение о принадлежности подборки генеральной совокупы либо о однородности выборок меж собой.
2. При наличии подборки, удовлетворяющей требованиям относительно ее пригодности для установления закона распределения перед тем, как приступить к определению статистических черт, нужно проверить, принадлежат ли к данной выборке ее члены, резко отличающиеся от большинства данных, если таковые имеются. Таковая проверка строго неотклонима, потому что хоть какое неправильное решение в отношении резко различающихся результатов приводит к искажению вида кривой закона распределения и к следующим ошибкам, о которых уже говорилось выше. Описанная проверка также осуществляется при помощи соответственных критериев: аспекта Груббса (для малых выборок), аспекта Ирвина и неких остальных. В качестве нулевой догадки во всех вариантах принимается предположение о том, что резко выделяющиеся результаты принадлежат данной выборке.
3. Заключительной и самой трудозатратной проверкой является проверка гипотез о виде функции распределения либо, что то же, о согласовании предполагаемого закона теоретического распределения эмпирическому. Эта проверка осуществляется при помощи так именуемых критериев согласия. Есть аспекты для проверки соответствия как предполагаемому нормальному либо логарифмически-нормальному закону распределения, так и хоть какому другому закону распределения.
Более применяемыми при практических расчетах являются последующие аспекты:
а) аспект Пирсона (χ2
); он справедлив при огромных размерах выборок и для всех законов распределения;
б) аспект Колмогорова-Смирнова (Du); этот аспект употребляется для проверки догадки о согласовании эмпирического распределения хоть какому теоретическому закону распределения с заблаговременно известными параметрами, что накладывает ограничения на его внедрение. В то же время Du является наиболее массивным, чем аспект χ2
;
в) аспект Крамера-Мизеса (w2
); данный аспект употребляется для размеров выборок 50 £n£ 200 и является наиболее массивным, чем χ2
, но, при его применении требуется больший размер вычислений. Потому при n > 200 этот аспект целенаправлено применять лишь в тех вариантах, когда проверки догадки по остальным аспектам не приводят к бесспорным результатам;
г) аспект Шапиро-Уилкса (W); он предназначен для проверки догадки о обычном либо логарифмически обычном законе распределения при ограниченном объеме подборки (n£ 50) и является наиболее массивным, чем остальные аспекты.
Укрупненно порядок проведения статистической обработки инфы можно представить последующим образом: опосля решения вопросца о объеме подборки и принадлежности к ней резко различающихся результатов, строится гистограмма, рассчитываются статистические свойства исследуемой случайной величины, и устанавливается законее распределения.
При решении технических и экономических задач существует довольно широкий круг законов распределения, которым подчиняются те либо другие процессы. К ним относятся законы Вейбулла, Релея, экспоненциальный, гамма-распределения, но, самыми всераспространенными являются обычный (Гаусса) и логарифмически-нормальный законы распределения. Получив математическое выражение закона распределения, другими словами соотношение, устанавливающее связь меж вероятными значениями случайной величины и надлежащими им вероятностями, можно утверждать, что с вероятностной точки зрения, случайная величина описана стопроцентно.
]]>

