Загрузка...
Учебная работа. Курсовая работа: Предмет и задачи статистики
Статистические дисциплины играют важную роль в системе экономического образования. Для общеэкономических специальностей, статистика является основой для разработки и совершенствования способов экономического анализа. Сама же статистика — самостоятельная общественная наука, имеющая собственный предмет и способ исследования. понятие «статистика» происходит от латинского слова «status», которое в переводе, значит — положение, состояние, порядок явлений. Эта наука, изучающая положение дел в государстве. Основная её задачка – это сбор цифровых данных, их обобщение и переработка. Зависимо от объекта исследования статистика как наука разделяется на социальную, демографическую, экономическую, промышленную, торговую, банковскую, финансовую, мед и т.д. Общие характеристики статистических данных, независимо от их природы и способы их анализа рассматриваются математической статистикой и общей теорией статистики.
Предмет статистики.
Под предметом статистики понимается численная сторона массовых публичных явлений в неизменной связи с их содержанием либо количественной стороной, также количественное выражение закономерностей публичного развития в определенных критериях места и времени. Одной из соответствующих особенностей статистики будет то, что при исследовании количественной стороны публичных явлений и действий она постоянно показывает высококачественные индивидуальности исследуемых явлений, т.е. изучает количество в неразрывной связи, единстве с качеством (свойство – это характеристики, присущие предмету либо явлению, которые различают данный предмет либо явление от остальных).
Предмет статистики исследуется с помощью определённых понятий, таковых как: статистическая совокупа, единица совокупы, признак, статистический показатель, система статистических характеристик. Статистической совокупой именуют совокупа объектов либо явлений публичной жизни, объединённых общей связью. Первичным элементом статистической совокупы, являющимся носителем признаков, подлежащих регистрации, и основой ведущегося при обследовании счёта – является единица совокупы. Общие признаки непременно должны находиться посреди исследуемых объектов, для того, чтоб можно было выделить статистическую совокупа либо даже несколько рядов статистической совокупы для этих объектов. совокупа объектов, имеющих один либо больше общих признаков, именуется однородной. А совокупа, включающая в себя различные типы и явления, является разнородной. В принципе, неважно какая совокупа, по отношению к различным нюансам рассматриваемых явлений, быть может однородной и разнородной сразу. Средством анализа содержания этих отношений, определяется возможность использования общих черт. Определение состава статистической совокупы, отграничение частей различных совокупностей, достигаемое вместе с иными науками, — одна из более принципиальных задач статистики.
Система признаков употребляется для составления программки статистического наблюдения и следующей группировки материалов. К самим признакам относят соответствующие черты либо индивидуальности объектов, которые может быть охарактеризовать статистических величин. признаки, принимающие разные значения либо видоизменения у отдельных единиц совокупы, именуются варьирующими, а отдельные их значения либо видоизменения — вариациями. Варьирующие признаки разделяются на атрибутивные (высококачественные) и количественные. признак именуется атрибутивным, если отдельные его значения (варианты) выражаются в виде состояния, параметров и т.д., присущих явлению. К таковым признакам, выражающим присущие явлению характеристики, относятся: профессия, отраслевая принадлежность компаний и др. признак именуется количественным, если отдельные его значения (варианты) выражаются в виде чисел. По признаки, которые могут принимать лишь полностью определенные значения, меж которыми не могут иметь пространство промежные значения. К примеру, число членов семь и т.п. Варианты дискретных признаков обычно выражаются в виде целых чисел. Количественные признаки, которые могут в определенных границах принимать любые значения как целые, так и дробные, именуются непрерывными. Таковыми признаками являются, к примеру, возраст, стаж работы, вес поезда, скорость движения и т.п. Градация признаков на высококачественные и количественные довольно условна, т.к. постоянно существует неразрывная связь свойства и количества. признаки могут быть главные, определяющие социально-экономическое содержание действий, и второстепенные, наружные по отношению к сути изучаемых явлений, т.е. конкретно не связанные с внутренней структурой действий (экстенсивные признаки). Статистическая наука просит выделения в программках наблюдения и группировке сначала основных, главных признаков. Признаки бывают первичные, которые лежат в базе программки сбора первичных статистических материалов, и вторичные, характеризуемые в процессе обработки и анализа данных.
Статистический показатель – обобщённая численная черта явлений и действий в единстве с их высококачественной определённостью. Численность населения, удельный вес работающих людей в данной для нас численности – более обычный для осознания пример статистического показателя. Сводные экономические характеристики, относящиеся к сложному комплексу экономических явлений либо к разнообразным национально-хозяйственным действиям и объектам, именуют синтетическими (к примеру, валовый государственный продукт, государственный Доход, национальное достояние). Величина показателя определяется в итоге измерения объектов (частей) и изменяется зависимо от методологических особенностей его построения, обусловленных в свою очередь степенью охвата изучаемых действий. характеристики именуются натуральными, когда они выражены в единицах счета либо в разных физических единицах измерения (в мерах линейных, площади, размера, массы и др.), и валютными, либо стоимостными, когда они представляют собой валютную оценку экономических объектов. Условно, статистические характеристики можно поделить и на объёмные и высококачественные. Себестоимость единицы изделия – это высококачественный статистический признак. Он даёт представление о способностях и закономерностях развития событий (сколько будет стоить партия данного продукта и даже вероятная Прибыль с его реализации). Характеристики, связанные с переменами величины совокупы объектов относят к объёмным показателям, т.к. они не влияют на свойство. совокупа взаимосвязанных характеристик, отображающих процессы публичной жизни в определённых критериях, образуют систему статистических характеристик. Эта система повсевременно совершенствуется, из-за конфигураций критерий жизни и системы экономических характеристик.
Способ статистики.
Существует две главных группы статистических способов: способы статистического наблюдения и способы обработки и анализа статистических данных. Входящие в состав способа статистического наблюдения отчётность, переписи и др. разрешают получить массовые и надёжные материалы о разных соц либо экономических явлениях. Группировки, балансовый способ, исчисление средних величин (способ средних), исчисление индексов (индексный способ), графический способ и т.д. — являются специфичными для статистики способами обработки данных. Огромное способ теории вероятности и способ математической статистики. Эти способы используются для конфигурации ошибки подборки, анализа связи меж факторами и оценки надёжности результатов. В процессе статистического исследования, статистические способы используются комплексно.
Разные специальные способы исследования, взаимосвязанные меж собой, образуют в собственной совокупы статистическую методологию. Важными составными элементами статистической методологии являются: 1)общее наблюдение; 2)группировки, применение обобщающих (сводных) черт; 3)анализ и обобщение статистических фактов и обнаружение закономерностей в изучаемых явлениях.
Статистическое исследование постоянно начинается с подготовки по организации этого исследования. работы по организации делятся на самостоятельные этапы либо стадии: статистическое наблюдение, сводка и обработка материалов, анализ данных. На первом шаге происходит сбор массовых статистических данных, при помощи первичного учёта и периодической регистрации. Первичный статистический учет, является научной, специально организованной регистрацией признаков каждой единицы совокупы и записью их в определенных документах. К статистическим данным, подходящим для обобщения, предъявляется ряд требований:
данные должны быть очень полными, но не обрывочными, случаем выхваченными;
данные должны быть полностью достоверными и точными;
данные должны соответствовать принципу единообразия, сопоставимости;
данные должны соответствовать принципу своевременности (сбор должен быть организован лишь в строго определенное время;
данные должны быть представлены так же в срочном порядке).
Объектом статистического наблюдения именуется та совокупа, о которой должны быть собраны нужные сведения. Объектом наблюдения быть может, к примеру, совокупа фермерских хозяйств республики (либо же какого-нибудь района), совокупа ВУЗ-ов, совокупа промышленных компаний и т.д. Единицей наблюдения именуют тот составной элемент объекта наблюдения, который является носителем признаков, подлежащих регистрации. В одном каком-либо наблюдении быть может не одна, а несколько единиц наблюдения. Так при переписи населения, к примеру, единицей наблюдения быть может либо человек (обитатель), либо семья, либо то и другое. Единицы наблюдения, как и объект в целом, владеют, обычно, обилием разных признаков. Все их учитывать нереально. Потому нужно найти какие признаки следует регистрировать в процессе наблюдения. Список признаков, регистрируемых в процессе наблюдения, именуют программкой статистического наблюдения. вместе с составлением списка признаков, включаемых в программку наблюдения, принципиальное осознание всеми участвующими в наблюдении лицами. В этих целях нередко в формулировку вопросцев врубается так именуемый подсказ, т.е. варианты вероятных ответов. Статистическое наблюдение может делается в 2-ух главных формах: в форме отчетности и в форме специально организованных статистических обследований. Особые статистические обследования освещают моменты, не охватываемые статистической отчетностью, служат средством для проверки и анализа материалов данной для нас отчетности, дают доп материал как для национально-хозяйственного прогнозирования и оперативных мероприятий, так и для зания
закономерностей развития экономики. Для исследования особенностей и закономерностей публичных явлений используются разные виды и методы сбора статистических сведений. Зависимо от задач исследования и определенных критерий статистическое наблюдение быть может единовременным либо текущим. Единовременное наблюдение — запись признаков единиц наблюдения, приуроченная к данному «критичному моменту» времени. Единовременное наблюдение либо учет состояния проводится через некие периоды времени, обхватывает продолжительно существующую совокупа. Такое наблюдение проводится для определения численности, состава и высококачественных особенностей совокупы. программка сбора сведений в этом случае обязана быть в главном аналогичной содержанию предыдущих единовременных наблюдений. Текущее наблюдение либо текущий учет ведется для определения измерений состояния явления. Единицы наблюдения и их признаки регистрируются в момент появления либо же в ближний опосля этого момент времени.
Материалы единовременного и текущего наблюдений взаимно дополняют друг друга; создается возможность получения данных на хоть какой момент времени либо за хоть какой период времени. Сплошное наблюдение — учет всех без исключения единиц в границах данной совокупы, к примеру перепись всех видов оборудования либо материалов в данном предприятии. Материалы сплошного наблюдения разрешают выделить в составе изучаемой массе единицы отменно однородной группы и найти по каждой группе средние величины по более значимым признакам. Единовременное и текущее наблюдения осуществляются в форме сплошного наблюдения, если нужно получить сведения о объеме изучаемых явлений. Организация сплошного наблюдения не постоянно вероятна и целесообразна, в особенности для контроля за качеством продукции. В этом случае сплошное наблюдение приводит к исключению из сферы практического использования массы продукции компаний. Потому нужно производить несплошное (частичное) наблюдение — учесть лишь часть единиц совокупы, по которой составляют наблюдение имеет определенные достоинства по сопоставлению со сплошным наблюдением:
требуется существенно меньше издержек труда и средств в связи с уменьшением числа обследуемых единиц;
данные могут быть собраны в наиболее недлинные сроки и по наиболее широкой программке, чтоб в данных границах всесторонне раскрыть индивидуальности изучаемой совокупы, провести наиболее глубочайшее научное исследование;
данные несплошного наблюдения привлекаются для контроля материалов сплошного наблюдения;
несплошное наблюдение обязано быть репрезентативным (презентабельным).
Обследуемые единицы отбираются так, чтоб, делая упор на приобретенные по сиим единицам данные, составить правильное части совокупы. Монографическое наблюдение — детализированное описание маленького числа единиц совокупы. Типическая монография, как один из методов исследования особенностей единиц совокупы, предугадывает отбор из состава всей совокупы отменно однородных единиц 1-го типа. Собираются сведения по 1-3 единицам с персональными значениями признака, близкими к обычным значениям признака в группе. К числу недочетов типической монографии относится личный выбор единиц наблюдения, когда руководствуются лишь общим представлением о их соответствующих особенностях. Не считая того, число отобранных единиц невелико, не соответствуют численности самой группы, и приобретенные данные не разрешают изучить распределение единиц (состав, долю) в границах отдельной группы. Большая уверенность в репрезентативности данных, приобретенных типической монографией, достигается, если выбор единиц основан на данных ранее выполненных сплошных наблюдений. Анкетный метод предугадывает раздачу анкет (время от времени анкеты публикуют) всем единицам совокупы для особых обследований, к примеру с целью исследования регулярности доставки почтовой корреспонденции, воззрений по отдельным вопросцам. Анкеты заполняются добровольно и потому не постоянно обеспечивается репрезентативность подборки. программка анкетного обследования содержит узенький круг вопросцев, ответы на которые нередко дают лишь заинтригованные лица. Огромное распространение получает способ интервью, когда опрос ведется методом личного общения по специально разработанной программке. Таковой способ обширно применяется в социологических исследовательских работах. Более совершенным с научной точки зрения видом несплошного наблюдения является выборочное наблюдение. Выборочное наблюдение представляет собой таковой вид статистического наблюдения, при котором обследованию подвергается некая часть единиц изучаемой совокупы, отобранная в определенном строго научном порядке, с целью последущей свойства всей совокупы. Сплошное и несплошное статистическое наблюдение осуществляется разными методами: конкретным наблюдением, опросом и документированной записью. Источником сведений служит опрос. По способу регистрации фактов опрос имеет разновидности: экспедиционный метод, саморегистрация, корреспондентский метод и документированная запись. Экспедиционный метод предугадывает сбор сведений на месте появления факта. Особый регистратор производит опрос и сам записывает ответ. Этот метод обеспечивает точную информацию, но просит значимых издержек времени, труда и средств. Саморегистрация осуществляется с ролью специального регистратора на месте сбора сведений. Регистратор лишь объясняет порядок ответов на поставленные вопросцы в бланке, а ответы даются обычно представителями организаций и компаний. Этот метод просит значимых издержек времени и средств, также вербования высококлалифицированных статистических работников. Корреспондентский метод подразумевает рассылку статистическими и иными элементами управления специально разработанных бланков и инструкций по их наполнению хозяйствующим субъектам либо специально выделенным лицам корреспондентам для исследования определенного вопросца. Сведения поступают в установленные сроки по почте, телеграфом либо доставляются нарочным. метод не просит особенных издержек, но свойство инфы зависит от уровня познаний и степени подготовки корреспондентов. Документированная запись — основная форма статистического наблюдения является главным источником расчета статистических характеристик.
Собранные в процессе статистического наблюдения данные о величине признака единиц в изучаемой совокупы должны быть обработаны так, чтоб вышел четкий и серьезный ответ на все вопросцы, поставленные с целью исследования. Свойство начального статистического материала предназначает свойство обобщающих характеристик, приобретенных в итоге статистической обработки (статистической сводки). Даже при довольно совершенной организации статистического наблюдения могут встречаться в приобретенной статистической инфы отдельные ошибки либо погрешности, которые следует убрать, чтоб получить доброкачественный начальный статистический материал. Ошибки статистического наблюдения — расхождение реальных значений признаков единиц наблюдения с их величиной, зарегистрированной в процессе сбора сведений. Ошибки статистического наблюдения многообразны по происхождению и значения ошибок. По источнику происхождения различают ошибки ненамеренные и намеренные, а по значению — случайные и периодические. Случайными ошибками числятся такие погрешности в записи данных по отдельным единицам, в отношении которых подразумевают, что они могут с схожей вероятностью исказить результаты статистического наблюдения в обратные стороны. К ошибкам такового вида относятся ненамеренные ошибки – как следствие описок либо недостаточно ясного осознания регистратором сути регистрируемых признаков. Случайные ошибки при статистическом наблюдении массы единиц не оказывают существенного воздействия на конечные результаты обследования: в процессе статистической сводки собранных данных они обычно взаимопогашаются. Периодические ошибки искажают сведения по отдельным единицам наблюдения в одном направлении (преомнажают либо умаляют). К периодическим ошибкам относятся: пропуски единиц наблюдения, ошибки, возникающие в силу неисправности измерительных устройств, а время от времени и рвения отдельных лиц округлять величины при устном опросе. к примеру, при недокументированном сборе сведений вероятны округления возраста, стажа работы, зарплаты. Все периодические ошибки являются намеренными ошибками и не погашаются в процессе статистической сводки. К ошибкам статистического наблюдения относятся ошибки, возникающие в процессе организации выборочного наблюдения, именуемые ошибками консульства, либо репрезентативности. Основное
1) сравниваются ответы на разные вопросцы 1-го и такого же формуляра, к примеру сопоставляются в бланке переписи населения сведения о профессии, возрасте, семейном положении;
2) сопоставляются записи, относящиеся к отчетному периоду, с подобными записями предыдущих периодов либо же с плановыми данными отчетного периода;
3) сравниваются фактические данные статистического наблюдения с разработанными нормативами: издержек времени, удельного расхода материалов и др.;
4) сопоставляются данные проведенных статистических наблюдений с плодами особых наблюдений выборочного нрава, в силу собственных особенностей, позволяющих получить наиболее полные данные по отобранной массе единиц.
В итоге первой стадии статистического исследования – статистического наблюдения получают сведения о каждой единице совокупы. задачка 2-ой стадии статистического исследования заключается в том, чтоб упорядочить и обобщить первичный материал, свести его в группы и на данной для нас базе отдать обобщенную характеристику совокупы. Этот шаг в статистике именуется сводкой. Различают ординарную сводку (подсчет лишь общих итогов) и статистическую группировку. Статистическая группировка сводится к расчленению совокупы на группы по существенному для единиц совокупы признаку. Структурные группировки имеют огромное практическое к примеру в области улучшения использования главных фондов, увеличения производительности труда, улучшения свойства продукции и т.д. Группировки, которые используются для исследования связи меж явлениями, именуются аналитическими. Используя аналитические группировки, до этого всего определяют факторные и действенные признаки изучаемых явлений. Факторные — это признаки, оказывающие воздействие на остальные, связанные с ними признаки. Действенные -признаки, которые меняются под воздействием факторных. Чтоб изучить связь меж отобранными признаками при помощи способа аналитических группировок, нужно произвести группировку единиц совокупы по факторному признаку и по каждой группе вычислить среднее наличие либо отсутствие связи. Группировка дозволяет получить такие результаты, по которым можно выявить состав совокупы, соответствующие черты и характеристики обычных явлений, найти закономерности и связи.
Первым и более обычным методом обобщения статистических данных являются ряды распределения. Статистическим распределения именуют численное распределение единиц совокупы по изучаемому признаку. Зависимо от признака ряды могут быть вариационные (количественные) и атрибутивные. Вариационные ряды могут быть дискретными либо интервальными. Дискретный ряд распределения — это ряд, в каком численное распределение признака выражено одним конечным числом. Интервальный ряд распределения — это ряд, в каком значения признака заданы в виде интервала. При построении интервальных рядов распределения нужно найти, какое число групп следует образовать и какие взять интервалы (равные, неравные, закрытые, открытые). Эти вопросцы решаются на базе экономического анализа сути изучаемых явлений, поставленной цели и нрава конфигураций признака. Интервалы не должны быть очень широкими и очень узенькими, т.к. это приведёт к искажению естественной картины данных.
На каждой стадии статистического исследования проводится проверка достоверности статистических данных. В процессе анализа обычно совершается доборная обработка материалов (перегруппировка, доп исчисление и т.д.). Проводится сопоставление данных для различных периодов времени, для разных объектов, инсталлируются предпосылки явлений, даётся общее описание фактов и разъяснение закономерностям, выделяемым, при помощи предыдущих способов. Тем, статистический анализ – это оканчивающее звено статистического исследования. Результаты анализа употребляются при разработке вопросцев экономической теории, прогнозировании и организации работы компаний. От корректности выводов и прогнозов зависит предстоящий фуррор компании, корректность решений и так дальше. Так, к примеру, правильно проведённый анализ, дающий точную и достоверную информацию о состоянии рынка услуг в сфере туризма и рекреации, быть может применен туроператорскими фирмами для разработки новейших, удовлетворяющих Спрос возможных потребителей и прибыльных самим фирмам, поставщикам услуг и работникам (занятым в данной сфере) турпродуктов либо турпакетов.
Расчётная часть.
Расчёт характеристик варианты.
Вариация является одной из важных категорий, используемых в статистической науке. Явления, подверженные варианты лежат в области исследования статистической науки, в то время как явления постоянные, статичные, неизменные в статистике не рассматриваются. Вариация – это принятие единицами совокупы либо их группами разных, различающихся друг от друга, значений признака. Вариация является результатом действия на единицы совокупы огромного количества причин. Синонимами термина «вариация» являются понятия «изменение», «изменчивость», «вариативность». Необходимость в измерении варианты возникает из-за того, что в средней величине не проявляется степень колеблемости отдельных значений признаков (вариант) вокруг среднего уровня. Зависимо от однородности в совокупы, степень колеблемости быть может большенный либо малеханькой. Вариацией именуется изменчивость лишь тех явлений, на которые действуют наружные причины и предпосылки. Тогда как о явлениях, изменяющихся в силу собственной внутренней природы недозволено гласить, что они подвержены варианты. к примеру, рост человека, меняющийся в течении жизни.
Различие личных значений признака снутри изучаемой совокупы в статистике именуется вариацией признака. Она возникает в итоге того, что его личные значения складываются под совокупным воздействием различных причин, которые по-разному смешиваются в каждом отдельно взятом случае.
Средняя величина — это абстрактная, обобщающая черта признака изучаемой совокупы, но она не указывает строения совокупы, которое очень значительно для ее зания. Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены ли они поблизости либо существенно отклоняются от нее. В неких вариантах отдельные значения признака близко примыкают к средней арифметической и не много от нее различаются. В таковых вариантах средняя отлично представляет всю совокупа. В остальных, напротив, отдельные значения совокупы далековато отстают от средней, и средняя плохо представляет всю совокупа.
Колеблемость отдельных значений охарактеризовывают характеристики варианты. термин «вариация» произошел от латинского variatio –“изменение, колеблемость, различие”. Но не всякие различия принято именовать вариацией. Под вариацией в статистике соображают такие количественные конфигурации величины исследуемого признака в границах однородной совокупы, которые обоснованы перекрещивающимся воздействием деяния разных причин. Различают вариацию признака: случайную и периодическую. анализ периодической варианты дозволяет оценить степень зависимости конфигураций в изучаемом признаке от определяющих ее причин. К примеру, изучая силу и нрав варианты в выделяемой совокупы, можно оценить, как однородной является данная совокупа в количественном, а время от времени и высококачественном отношении, а как следует, как соответствующей является исчисленная средняя величина. Степень близости данных отдельных единиц хi к средней измеряется абсолютных, средних и относительных характеристик.
Абсолютные и средние характеристики варианты и методы их расчета.
Для свойства совокупностей и исчисленных величин принципиально знать, какая вариация изучаемого признака прячется за средним. Для свойства колеблемости признака употребляется ряд характеристик. Более обычный из их — размах варианты.
Размах варианты — это разность меж большим (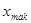
) и минимальным (
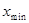) значениями вариантов.
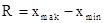
Достоинством этого показателя является простота расчёта. Поточнее охарактеризовывает вариацию признака показатель, основанный на учёте всех значений признака. К таковым показателям относится среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, представляющие из себя среднюю арифметическую из отклонений личных значений признака от средней арифметической.
Чтоб отдать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение d, которое учитывает различие всех единиц изучаемой совокупы.
Среднее линейное отклонение определяется как средняя арифметическая из отклонений личных значений от средней, без учета знака этих отклонений:
.
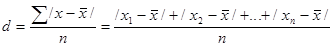порядок расчета среднего линейного отличия последующий:
1) по значениям признака исчисляется средняя арифметическая:
;
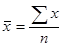2) определяются отличия каждой варианты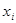 
от средней 
;
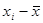3) рассчитывается сумма абсолютных величин отклонений: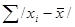 
;
4) сумма абсолютных величин отклонений делится на число значений:
.
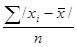Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:
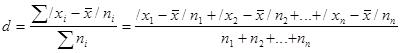
порядок расчета среднего линейного отличия взвешенного последующий:
1) рассчитывается средняя арифметическая взвешенная:
;
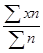2) определяются абсолютные отличия вариант от средней //;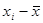
3) приобретенные отличия множатся на частоты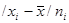 
;
4) находится сумма взвешенных отклонений без учета знака:
;
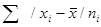5) сумма взвешенных отклонений делится на сумму частот:
.
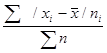Расчет дисперсии и среднего квадратического отличия по личным данным
и в рядах распределения.
Главными обобщающими показателями варианты в статистике являются дисперсии и среднее квадратическое отклонение.
Дисперсия — это средняя арифметическая квадратов отклонений всякого значения признака от общей средней. Дисперсия обычно именуется средним квадратом отклонений и обозначается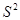 
. Зависимо от начальных данных дисперсия может рассчитываться по средней арифметической обычный либо взвешенной:
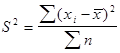— дисперсия невзвешенная (обычная);
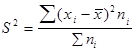— дисперсия взвешенная.
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается S:
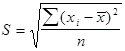— среднее квадратическое отклонение невзвешенное;
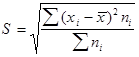— среднее квадратическое отклонение взвешенное.
Среднее квадратическое отклонение — это обобщающая черта абсолютных размеров варианты признака в совокупы. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.).
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает собой всю представляемую совокупа.
Вычислению среднего квадратического отличия предшествует расчет дисперсии.
порядок расчета дисперсии взвешенную:
1) определяют среднюю арифметическую взвешенную
;
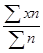2) определяются отличия вариант от средней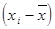 
;
3) возводят в квадрат отклонение каждой варианты от средней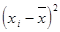 
;
4) множат квадраты отклонений на веса (частоты)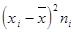 
;
5) суммируют приобретенные произведения
;
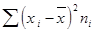6) Полученную сумму делят на сумму весов
.
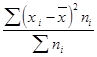Расчет дисперсии по формуле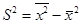 
по личным данным и в рядах распределения.
техника вычисления дисперсии сложна, а при огромных значениях вариант и частот быть может массивной. Расчеты можно упростить, используя характеристики дисперсии.
Характеристики дисперсии.
Уменьшение либо повышение весов (частот) варьирующего признака в определенное число раз дисперсии не изменяет.
Уменьшение либо повышение всякого значения признака на одну и ту же постоянную величину А дисперсии не изменяет.
Уменьшение либо повышение всякого значения признака в некое число раз к соответственно уменьшает либо наращивает дисперсию в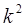 
раз, а среднее квадратическое отклонение — в к раз.
Дисперсия признака относительно случайной величины постоянно больше дисперсии относительно средней арифметической на квадрат разности меж средней и случайной величиной: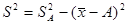 
. Если А равна нулю, то приходим к последующему равенству: 
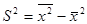, т.е. дисперсия признака равна разности меж средним квадратом значений признака и квадратом средней.
Каждое свойство при расчете дисперсии быть может использовано без помощи других либо в сочетании с иными.
порядок расчета дисперсии обычный:
1) определяют среднюю арифметическую ;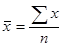
2) возводят в квадрат среднюю арифметическую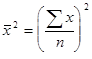
;
3) возводят в квадрат каждую варианту ряда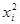 
;
4) находим сумму квадратов вариант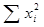 
;
5) делят сумму квадратов вариант на их число, т.е. определяют средний квадрат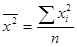 
;
6) определяют разность меж средним квадратом признака и квадратом средней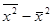 
.
Расчет дисперсии в интервальном ряду распределения.
порядок расчета дисперсии взвешенной (по формуле ):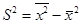
определяют среднюю арифметическую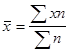 
;
возводят в квадрат полученную среднюю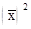 
;
возводят в квадрат каждую варианту ряда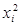 
;
множат квадраты вариант на частоты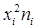 
;
суммируют приобретенные произведения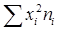 
;
делят полученную сумму на сумму весов и получают средний квадрат признака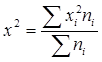 
;
определяют разность меж средним значением квадратов и квадратом средней арифметической, т.е. дисперсию .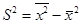
характеристики относительного рассеивания.
Для свойства меры колеблемости изучаемого признака исчисляются характеристики колеблемости в относительных величинах. Они разрешают ассоциировать нрав рассеивания в разных распределениях (разные единицы наблюдения 1-го и такого же признака в 2-ух совокупностях, при разных значениях средних, при сопоставлении разноименных совокупностей). Расчет характеристик меры относительного рассеивания производят как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.
1. Коэффициент осцилляции отражает относительную колеблемость последних значений признака вокруг средней.
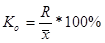(1)
2. Относительное линейное отклонение охарактеризовывает долю усредненного значения абсолютных отклонений от средней величины.
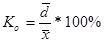(2)
3. Коэффициент варианты.
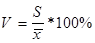(3)
Беря во внимание, что среднеквадратическое отклонение дает обобщающую характеристику колеблемости всех вариантов совокупы, коэффициент варианты является более всераспространенным показателем колеблемости, применяемым для оценки типичности средних величин. При всем этом исходят из того, что если V больше 40 %, то это гласит о большенный колеблемости признака в изучаемой совокупы.
Ряды Динамики.
установление вида ряда динамики.
Основная цель статистического исследования динамики коммерческой деятель состоит в выявлении и измерении закономерностей их развития во времени. Это достигается средством построения и анализа статистических рядов динамики.
Рядами динамики именуются статистические данные, отображающие развитие изучаемого явления во времени. В любом ряду динамики имеются два главных элемента: показатель времени t; надлежащие им уровни развития изучаемого явления у. В качестве показаний времени в рядах динамики выступают или определенные даты (моменты) времени, или отдельные периоды (годы, кварталы, месяцы, день).
Уровни рядов динамики показывают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными либо средними величинами.
Зависимо от нрава изучаемого явления уровни рядов динамики могут относиться либо к определенным датам (моментам) времени, либо к отдельным периодам. В согласовании с сиим, ряды динамики разделяются на моментные и интервальные.
Моментные ряды динамики показывают состояние изучаемых явлений на определенные даты (моменты) времени.
Примером моментного ряда динамики является последующая информация о списочной численности работников компании N в 1994 г.:
Дата
1.01
1.04
1.07
1.10
1.01
Год
1994 г.
1994 г.
1994 г.
1994 г.
1995 г.
Число работников, чел.
192
190
195
198
200
Индивидуальностью моментного ряда динамики будет то, что в его уровни могут заходить одни и те же единицы изучаемой совокупы. Так, основная часть персонала компании N, составляющая списочную численность на 1.01.1994г., продолжающая работать в течение данного года, отображена в уровнях следующих периодов. Потому при суммировании уровней моментного ряда динамики может появиться повторный счет.
Интервальные ряды динамики показывают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени.
Примером интервального ряда динамики могут служить данные о розничном товарообороте магазина в 1990-1994 гг.:
Год
1990
1991
1992
1993
1994
Размер розничного товарооборота, тыс. руб.
885,7
932,6
980,1
1028,7
1088,4
Индивидуальностью интервального ряда динамики будет то, что любой его уровень складывается из данных за наиболее недлинные интервалы времени. К примеру, суммируя товарооборот за 1-ые три месяца года, получают его размер за I квартал, а сумма товарооборота 4 кварталов дает размер товарооборота за год и т.д.
Ряды динамики могут быть полными и неполными.
Полный ряд — ряд динамики, в каком одноименные моменты времени либо периоды времени строго следуют один за остальным в календарном порядке либо равноотстоят друг от друга.
Неполный ряд динамики — ряд, в каком уровни зафиксированы в неравноотстоящие моменты либо периоды времени.
Пример.
Численность населения СССР
Для того, чтоб анализ ряда был беспристрастен, нужно учесть действия, приводящие к несопоставимости уровней ряда и употреблять приемы обработки рядов для приведения их в сопоставимый вид.
Более соответствующие случаи несопоставимости уровней ряда динамики:
Территориальные конфигурации объекта исследования, к которому относится изучаемый показатель (изменение границ городского района, пересмотр административного деления области и т.д.).
Разновеликие интервалы времени, к которым относится показатель. Так, к примеру, в феврале — 28 дней, в марте — 31 денек, анализируя конфигурации показателя по месяцам, нужно учесть разницу в количестве дней.
Изменение даты учета. к примеру, численность поголовья скота в различные годы могла определяться по состоянию на 1 января либо на 1 октября, что в данном случае приводит к несопоставимости.
Изменение методологии учета либо расчета показателя.
Изменение цен.
Изменение единиц измерения.
Определение среднего уровня ряда динамики.
В качестве обобщенной свойства уровней ряда динамики служит средний уровень ряда динамики 
. Зависимо от типа ряда динамики употребляются разные расчетные формулы.
Интервальный ряд абсолютных величин с равными периодами (интервалами времени):
Моментный ряд с равными интервалами меж датами:
Моментный ряд с неравными интервалами меж датами:
где 
— уровни ряда, сохраняющиеся без конфигурации в протяжении интервала времени 
.
Характеристики конфигурации уровней ряда динамики.
Одним из важных направлений анализа рядов динамики является исследование особенностей развития явления за отдельные периоды времени.
С данной для нас целью для динамических рядов рассчитывают ряд характеристик:
К — темпы роста;
— абсолютные приросты;
— темпы прироста.
Темп роста — относительный показатель, получающийся в итоге деления 2-ух уровней 1-го ряда друг на друга. Темпы роста могут рассчитываться как цепные, когда любой уровень ряда сопоставляется с предыдущим ему уровнем: 
, или как базовые, когда все уровни ряда сопоставляются с одним и этим же уровнем 
, избранным за базу сопоставления:
. Темпы роста могут быть представлены в виде коэффициентов или в виде процентов.
Абсолютный прирост — разность меж 2-мя уровнями ряда динамики, имеет ту же размерность, что и уровни самого ряда динамики. Абсолютные приросты могут быть цепными и базовыми, зависимо от метода выбора базы для сопоставления:
цепной абсолютный прирост — 
;
базовый абсолютный прирост — 
.
Для относительной оценки абсолютных приростов рассчитываются характеристики темпов прироста.
Темп прироста — относительный показатель, показывающий на сколько процентов один уровень ряда динамики больше (либо меньше) другого, принимаемого за базу для сопоставления.
Базовые темпы прироста: 
.
Цепные темпы прироста: 
.
и 
— абсолютный базовый либо цепной прирост;
— уровень ряда динамики, избранный за базу для определения базовых абсолютных приростов;
— уровень ряда динамики, избранный за базу для определения i-го цепного абсолютного прироста.
Существует связь меж темпами роста и прироста:
К = К — 1 либо К = К — 100 % (если темпы роста определены в процентах).
Если поделить абсолютный прирост (цепной) на темп прироста (цепной) за соответственный период, получим показатель, именуемый — абсолютное .
Определение среднего абсолютного прироста, средних темпов роста и прироста.
По показателям конфигурации уровней ряда динамики (абсолютные приросты, темпы роста и прироста), приобретенным в итоге анализа начального ряда, могут быть рассчитаны обобщающие характеристики в виде средних величин — средний абсолютный прирост, средний темп роста, средний темп прироста.
Средний абсолютный прирост быть может получен по одной из формул:
либо 
,
где n — число уровней ряда динамики;
— 1-ый уровень ряда динамики;
— крайний уровень ряда динамики;
— цепные абсолютные приросты.
Средний темп роста можно найти, пользуясь формулами:
где n — число рассчитанных цепных либо базовых темпов роста;
— уровень ряда, принятый за базу для сопоставления;
— крайний уровень ряда;
— цепные темпы роста (в коэффициентах);
— 1-ый базовый темп роста;
— крайний базовый темп роста.
Меж темпами прироста 
и темпами роста К существует соотношение = К — 1, аналогичное соотношение правильно и для средних величин.
Определение в рядах динамики
общей тенденции развития.
Определение уровней ряда динамики в протяжении долгого периода времени обосновано действием ряда причин, которые неоднородны по силе и направлению действия, оказываемого на изучаемое явление.
Рассматривая динамические ряды, пробуют поделить эти причины на повсевременно действующие и оказывающие определяющее действие на уровни ряда, формирующие основную тенденцию развития, и случайные причины, приводящие к краткосрочным изменениям уровней ряда динамики. Более принципиальна при анализе ряда динамики его основная тенденция развития, но нередко по одному только наружному виду ряда динамики ее установить нереально, потому употребляют особые способы обработки, дозволяющие показать основную тенденцию ряда. способы обработки употребляются как обыкновенные, так и довольно сложные. Простой метод обработки ряда динамики, используемый с целью установления закономерностей развития — способ укрупнения интервалов.
Сущность способа в том, чтоб от интервалов, либо периодов времени, для которых определены начальные уровни ряда динамики, перейти к наиболее длительным периодам времени и поглядеть, как уровни ряда меняются в этом случае.
Иной метод определения тенденции в ряду динамики — способ скользящих средних. Сущность способа состоит в том, что фактические уровни ряда заменяются средними уровнями, вычисленными по определённому правилу, к примеру:
— начальные либо фактические уровни ряда динамики заменяются средними уровнями:
…
…
…
В итоге выходит сглаженный ряд, состоящий из скользящих пятизвенных средних уровней 
. Меж расположением уровней 
и 
устанавливается соответствие:
— — 
— — ,
сглаженный ряд короче начального на число уровней 
, где k — число уровней, избранных для определения средних уровней ряда.
Выравнивание способом скользящих средних можно создавать по четырём, 5 либо другому числу уровней ряда, используя надлежащие формулы для усреднения начальных уровней.
Приобретенные при всем этом средние уровни именуются четырёхзвенными скользящими средними, пятизвенными скользящими средними и т.д.
При выравнивании ряда динамики по чётному числу уровней производится доборная операция, именуемая центрированием, так как, при вычислении скользящего среднего, к примеру по четырём уровням, 
относится к временной точке меж моментами времени, когда были зафиксированы фактические уровни 
и 
. Схема вычислений и расположений уровней сглаженного ряда становится труднее:
… — начальные уровни;
— — 
… — сглаженные уровни;
— — 
… — центрированные сглаженные уровни;
.
способ скользящих средних не дозволяет получить численные оценки для выражения главный тенденции в ряду динамики, давая только приятное графическое определения тенденции развития в ряду динамики является способ аналитического сглаживания. При всем этом способе начальные уровни ряда динамики 
заменяются теоретическими либо расчетными , которые представляют из себя некую довольно ординарную математическую функцию времени, выражающую общую тенденцию развития ряда динамики. Почаще всего в качестве таковой функции выбирают прямую, параболу, экспоненту и др.
к примеру, 
,
где 
— коэффициенты, определяемые в способе аналитического сглаживания;
— моменты времени, для которых были получены начальные и надлежащие теоретические уровни ряда динамики, образующие прямую, определяемую коэффициентами .
Расчет коэффициентов ведется на базе способа меньших квадратов:
Если заместо подставить 
(либо соответственное выражение для остальных математических функций), получим:
Это функция 2-ух переменных 
(все 
и 
известны), которая при определенных добивается минимума. Из этого выражения на базе познаний, приобретенных в курсе высшей арифметики о экстремуме функций n переменных, получают значения коэффициентов .
Для прямой:
где n — число моментов времени, для которых были получены начальные уровни ряда .
Если заместо абсолютного времени избрать условное время таковым образом, чтоб 
, то записанные выражения для определения упрощаются:
Выборочное наблюдение.
Статистическое исследование может осуществляться по данным несплошного наблюдения, основная цель которого состоит в получении черт изучаемой совокупы по обследованной ее части. Одним из более всераспространенных в статистике способов, применяющих несплошное наблюдение, является выборочный способ.
Под выборочным понимается способ статистического исследования, при котором обобщающие характеристики изучаемой совокупы инсталлируются по некой ее части на базе положений случайного отбора. При выборочном способе обследованию подвергается сравнимо маленькая часть всей изучаемой совокупы (обычно до 5 — 10%, пореже до 15 — 25%). При всем этом подлежащая исследованию статистическая совокупа, из которой делается отбор части единиц, именуется генеральной совокупой. Отобранная из генеральной совокупы некая часть единиц, подвергающаяся обследованию, именуется выборочной совокупой либо просто подборкой.
инфы, уменьшает ошибки регистрации.
В проведении ряда исследовательских работ выборочный способ является единственно вероятным, к примеру, при контроле свойства продукции (продукта), если проверка сопровождается ликвидированием либо разложением на составные части обследуемых образцов (определение сахаристости фруктов, клейковины печеного хлеба, установление носкости обуви, прочности тканей на разрыв и т.д.).
Проведение исследования социально — экономических явлений выборочным способом складывается из ряда поочередных шагов:
1) обоснование (в согласовании с задачками исследования) необходимости внедрения выборочного способа;
2) составление программки проведения статистического исследования выборочным способом;
3) решение организационных вопросцев сбора и обработки начальной инфы;
4) установление толики подборки, т.е. части подлежащих обследованию единиц генеральной совокупы;
5) обоснование методов формирования выборочной совокупы;
6) воплощение отбора единиц из генеральной совокупы для их обследования;
7) фиксация в отобранных единицах (пробах) изучаемых признаков;
8) статистическая обработка приобретенной в выборке инфы с определением обобщающих черт изучаемых признаков;
9) определение количественной оценки ошибки подборки;
10) распространение обобщающих выборочных черт на генеральную совокупа.
В генеральной совокупы толика единиц, владеющих изучаемым признаком, именуется генеральной толикой (обозначается р), а средняя величина изучаемого варьирующего признака — генеральной средней (обозначается 
).
В выборочной совокупы долю изучаемого признака именуют выборочной толикой, либо частостью (обозначается 
), а среднюю величину в выборке — выборочной средней (обозначается 
).
Ошибка подборки — это беспристрастно возникающее расхождение меж чертами подборки и генеральной совокупы. Она зависит от ряда причин: степени варианты изучаемого признака, численности подборки, способом отбора единиц в выборочную совокупа, принятого уровня достоверности результата исследования.
Определение ошибки выборочной средней.
При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле:
,
где 
— средняя ошибка выборочной средней;
— дисперсия выборочной совокупы;
n — численность подборки.
При бесповторном отборе она рассчитывается по формуле:
,
где N — численность генеральной совокупы.
Определение ошибки выборочной толики.
При повторном отборе средняя ошибка выборочной толики рассчитывается по формуле:
,
где 
— выборочная толика единиц, владеющих изучаемым признаком;
— число единиц, владеющих изучаемым признаком;
— численность подборки.
При бесповторном методе отбора средняя ошибка выборочной толики определяется по формулам:
Предельная ошибка подборки 
связана со средней ошибкой подборки отношением:
.
При всем этом t как коэффициент кратности средней ошибки подборки зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки подборки.
Предельная ошибка подборки при бесповторном отборе определяется по последующим формулам:
,
.
Предельная ошибка подборки при повторном отборе определяется по формуле:
,
.
Малая подборка.
При контроле свойства продуктов в экономических исследовательских работах совокупа появляется из сравнимо маленького числа единиц генеральной совокупы. Размер малой подборки обычно не превосходит 30 единиц и может доходить до 4 — 5 единиц.
Средняя ошибка малой подборки 
рассчитывается по формуле:
,
где 
— дисперсия малой подборки.
При определении дисперсии число степеней свободы равно n-1:
.
Предельная ошибка малой подборки 
определяется по формуле
При всем этом
.
методы распространения черт подборки на генеральную совокупа.
Выборочный способ почаще всего применяется для получения черт генеральной совокупы по подходящим показателям подборки. Зависимо от целей исследовательских работ это осуществляется либо прямым пересчётом характеристик подборки для генеральной совокупы, либо средством расчёта поправочных коэффициентов.
метод прямого пересчёта. Он заключается в том, что характеристики выборочной толики либо средней 
распространяется на генеральную совокупа с учётом ошибки подборки.
Так, в торговле определяется количество поступивших в партии продукта необычных изделий. Для этого (с учётом принятой степени вероятности) характеристики толики необычных изделий в выборке множатся на численность изделий во всей партии продукта.
Метод поправочных коэффициентов. Применяется в вариантах, когда целью выборочного способа является уточнение результатов сплошного учета.
В статистической практике этот метод употребляется при уточнении данных каждогодних переписей скота, находящегося у населения. Для этого опосля обобщения данных сплошного учета практикуется 10%-ное выборочное обследование с определением так именуемого “процента недоучета”.
Так, к примеру, если в хозяйствах населения поселка по данным 10%-ной подборки было записанно 52 головы скота, а по данным сплошного учета в этом массиве числится 50 голов, то коэффициент недоучета составляет 4% [(2*50):100]. С учетом приобретенного коэффициента вносится поправка в общую численность скота, находящегося у населения данного поселка.
методы отбора единиц из генеральной совокупы.
В статистике используются разные методы формирования выборочных совокупностей, что обусловливается задачками исследования и зависит от специфичности объекта исследования.
Главным условием проведения выборочного обследования является предупреждение появления периодических ошибок, возникающих вследствие нарушения принципа равных способностей попадания в подборку каждой единицы генеральной совокупы. Предупреждение периодических ошибок достигается в итоге внедрения научно обоснованных методов формирования выборочной совокупы.
Есть последующие методы отбора единиц из генеральной совокупы:
1) личный отбор — в подборку отбираются отдельные единицы;
2) групповой отбор — в подборку попадают отменно однородные группы либо серии изучаемых единиц;
3) комбинированный отбор — это композиция личного и группового отбора.
методы отбора определяются правилами формирования выборочной совокупы.
Подборка быть может:
— собственно-случайная;
— механическая;
— типическая;
— серийная;
— комбинированная.
Фактически-случайная подборка заключается в том, что выборочная совокупа появляется в итоге случайного (ненамеренного) отбора отдельных единиц из генеральной совокупы. При всем этом количество отобранных в выборочную совокупа единиц обычно определяется исходя из принятой толики подборки.
Толика подборки есть отношение числа единиц выборочной совокупы n к численности единиц генеральной совокупы N, т.е.
.
Так, при 5%-ной выборке из партии продукта в 2 000 ед. численность подборки n составляет 100 ед. (5*2000:100), а при 20%-ной выборке она составит 400 ед. (20*2000:100) и т.д.
Механическая подборка заключается в том, что отбор единиц в выборочную совокупа делается из генеральной совокупы, разбитой на равные интервалы (группы). При всем этом размер интервала в генеральной совокупы равен оборотной величине толики подборки.
Так, при 2%-ной выборке отбирается любая 50-я единица (1:0,02), при 5%-ной выборке — любая 20-я единица (1:0,05) и т.д.
Таковым образом, в согласовании с принятой толикой отбора, генеральная совокупа вроде бы механически разбивается на равновеликие группы. Из каждой группы в подборку отбирается только одна единица.
Принципиальной индивидуальностью механической подборки будет то, что формирование выборочной совокупы можно выполнить, не прибегая к составлению списков. На практике нередко употребляют тот порядок, в каком практически располагаются единицы генеральной совокупы. к примеру, последовательность выхода готовых изделий с сборочного потока либо поточной полосы, порядок размещения единиц партии продукта при хранении, транспортировке, реализации и т.д.
Типическая подборка. При типической выборке генеральная совокупа сначала расчленяется на однородные типические группы. Потом из каждой типической группы собственно-случайной либо механической подборкой делается личный отбор единиц в выборочную совокупа.
Типическая подборка обычно применяется при исследовании сложных статистических совокупностей. к примеру, при выборочном обследовании производительности труда работников торговли, состоящих из отдельных групп по квалификации.
Принципиальной индивидуальностью типической подборки будет то, что она дает наиболее четкие результаты по сопоставлению с иными методами отбора единиц в выборочную совокупа.
Для определения средней ошибки типической подборки употребляются формулы:
повторный отбор
, 
бесповторный отбор
, 
Дисперсия определяется по последующим формулам:
, 
Серийная подборка. При серийной выборке генеральную совокупа делят на однообразные по размеру группы — серии. В выборочную совокупа отбираются серии. Снутри серий делается сплошное наблюдение единиц, попавших в серию.
При бесповторном отборе серий средняя ошибка выборочной серии определяется по формуле:
,
где 
— межсерийная дисперсия средних;
R — число серий в генеральной совокупы;
r — число отобранных серий.
В статистике различают одноступенчатые и многоступенчатые методы отбора единиц в выборочную совокупа.
При одноступенчатой выборке любая отобранная единица сходу же подвергается исследованию по данному признаку. Так обстоит дело при собственно-случайной и серийной выборке.
При многоступенчатой выборке создают подбор из генеральной совокупы отдельных групп, а из групп выбираются отдельные единицы. Так делается типическая подборка с механическим методом отбора единиц в выборочную совокупа.
Комбинированная подборка быть может двухступенчатой. При всем этом генеральная совокупа поначалу разбивается на группы. Потом создают отбор групп, а снутри крайних осуществляется отбор отдельных единиц.
Заключение.
Рассмотрев главные способы статистических расчетов, становится ясно видно, что таковая наука, как статистика оказывает неподменную помощь в решении муниципальных, экономических, социологических вопросцев и почти во всем содействует развитию данных наук и сфер деятель. Беря во внимание тот факт, что воздействие статистики распространяется на управленческую и экономическую деятельность компаний и компаний, можно заключить, что эта наука весьма принципиальна для функционирования, роста и удачливости компаний. В туристической сфере применение статистических данных и проведение статистического наблюдения, с следующим анализом приобретенной инфы, — неотъемлемая часть деятельности хоть какого компании. Это обосновывается тем, что туризм должен непрестанно смотреть за конфигурацией спроса на турпродукты, быть в курсе экономических и денежных конфигураций (как на мировом и муниципальном уровнях, так и на уровне раздельно взятых соц групп) и т.д. Для этого нужно повсевременно проводить исследования туристического рынка, производить сбор различных данных о популяции (их способностях и потребностях), также содействовать компаниям отыскать рациональные для их решения, встающих перед ними задач. Верно проведённый сбор, анализ данных и статистические расчёты разрешают обеспечить заинтригованные структуры и общественность информацией о развитии экономики, о направлении её развития, показать эффективность использования ресурсов, учитывать занятость населения и его трудоспособность, найти темпы роста цен и воздействие торговли на сам Рынок либо раздельно взятую сферу.
Перечень литературы
Финансовая статистика. 2-е издание, учебник/ под редакцией Ю. Н. Иванова. М. Инфра-М, 2001г.
М. Р. Ефимова. «Статистика». М. Инфра-М, 2002г.
А. М. Годин. «Статистика». М. «Дашков и К0», 2002г.
Формулы взяты из Веба (лекции по статистике).
]]>