Учебная работа. Реферат: Алгебра матриц
Определение. Прямоугольная таблица из m строк и n столбцов, заполненная некими математическими объектами, именуется 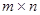 – матрицей.
– матрицей.
Мы будем разглядывать числовые матрицы. Числа, составляющие матрицу, именуются ее элементами. Для обозначения матрицы, как правило, употребляются круглые скобки. При записи, в общем виде элементы матрицы обозначаются одной буковкой с 2-мя индексами, из которых 1-ый показывает номер строчки, а 2-ой – номер столбца матрицы. к примеру, матрица
.
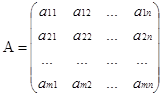 .
.
В сокращенной записи: А=(аij
); где аij
— действительные числа, i=1,2,…m;
j=1,2,…,n (коротко 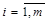 ,
, 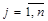 . ). Произведение
. ). Произведение 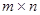 именуют размером матрицы.
именуют размером матрицы.
Матрица именуется квадратной порядка n, если число ее строк равно числу столбцов и равно n:
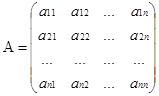
Упорядоченный набор частей а11
,а22
,…,аnn
именуется главной диагональю, в свою очередь, а1
n
,а2,
n
-1
,…,аn
1
– побочной диагональю матрицы. Квадратная матрица, элементы которой удовлетворяют условию: 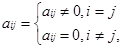
именуется диагональной, т.е. диагональная матрица имеет вид:
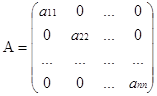
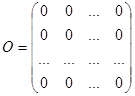
Диагональная матрица порядка n именуется единичной, если все элементы ее главной диагонали равны 1. Матрица хоть какого размера именуется нулевой либо нуль матрицей, если все ее элементы равны нулю. Единичная матрица обозначается буковкой Е, нулевая – О. Матрицы имеют вид:
.
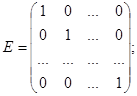
Линейные операции над матрицами
Определение. Суммой матриц А=(аij
) и B=(bij
) схожих размеров 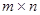 именуется матрица С=(сij
именуется матрица С=(сij
) тех же размеров, таковая что cij
=aij
+bij
для всех i и j.
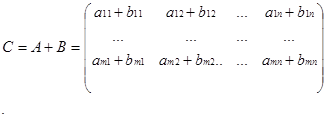 .
.
Таковым образом, чтоб сложить матрицы А и В, нужно сложить их элементы, стоящие на схожих местах. к примеру,
A + B = 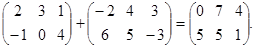 = C
= C
Определение. Произведение матрицы А на число l именуется матрица lА=(l аij
), получаемая умножением всех частей матрицы А на число l.
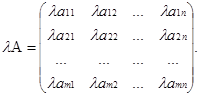
к примеру, если 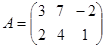 и l=5, то
и l=5, то 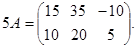
Разность матриц А и В можно найти равенством А-В=А+(-1)В.
Рассмотренные операции именуются линейными.
Отметим некие характеристики операций.
Пусть А,В,С – матрицы схожего размера; a,b — действительные числа.
А+В = В+А – коммутативность сложения.
(А+В)+С = А+(В+С) – ассоциативность сложения.
Матрица О, состоящая из нулей, играет роль нуля: А+О=А.
Для хоть какой матицы А существует обратная –А, элементы которой различаются от частей А знаком, при всем этом А+( -А)=О.
a(bА) = (ab)А = (aА)b. 6. (a+b)А = aА+bА.
7. a(А+В) = aА+aВ. 8. 1* А = А. 9. 0 * А = 0.
Умножение матриц
В матричной алгебре важную роль играет операция умножения матриц, это очень типичная операция.
Определение. Произведением матрицы А=(аij
) размера 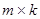 и прямоугольной матрицы B=(bij
и прямоугольной матрицы B=(bij
) размера 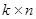 именуется прямоугольная матрица С=(сij
именуется прямоугольная матрица С=(сij
) размера 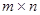 , таковая что cij
, таковая что cij
=ai
1
+b1
j
+ ai
2
+b2
j
+…+ aik
+bkj
; 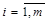 ,
, 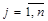 .
.
Таковым образом, элемент произведения матриц А и В, стоящий в i-ой строке и j-ом столбце, равен сумме произведений частей i-ой строчки первой матрицы А на надлежащие элементы j-ого столбца 2-ой матрицы В т.е.
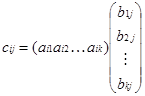 .
.
 Произведение С=АВ определено, если число столбцов матрицы А равно числу строк матрицы В. Это условие, также размеры матриц можно представить схемой:
Произведение С=АВ определено, если число столбцов матрицы А равно числу строк матрицы В. Это условие, также размеры матриц можно представить схемой:

 Разумеется, что операция умножения квадратных матриц постоянно определена.
Разумеется, что операция умножения квадратных матриц постоянно определена.
Примеры. Найдем произведения матриц АВ и ВА, если они есть.
1. 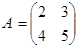 ,
, 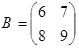 .
.
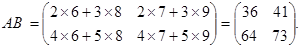
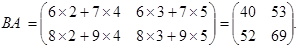
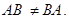
2. 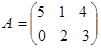 ,
, 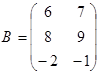 .
.
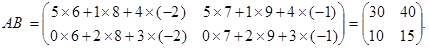
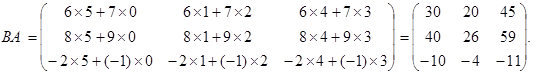
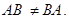
Таковым образом, коммутативный (переместительный) законумножения матриц, совершенно говоря, не производится, т.е. 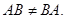 В личном случае коммутативным законом владеет произведение хоть какой квадратной матрицы А n-го порядка на единичную матрицу Е такового же порядка, т.е.
В личном случае коммутативным законом владеет произведение хоть какой квадратной матрицы А n-го порядка на единичную матрицу Е такового же порядка, т.е. 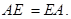
3. 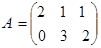 ,
, 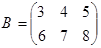 .
.
Для этих матриц произведение как АВ ,так и ВА не существует.
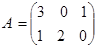 ,
, 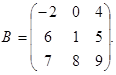
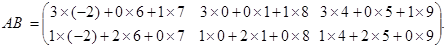
Получим 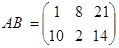 , ВА – не существует.
, ВА – не существует.
характеристики умножения матриц.
Пусть А,В,С – матрицы соответственных размеров (т.е. произведения матриц определены), l — действительное число. Тогда на основании определений операций и параметров реальных чисел имеют пространство последующие характеристики:
(АВ)С = А(ВС) – ассоциативность.
(А+В)С = АС+ВС – дистрибутивность.
А(В+С) = АВ+АС – дистрибутивность.
l(АВ) = (lА)В = А(lВ).
ЕА = АЕ = А, для квадратных матриц единичная матрица Е играет роль единицы.
Приведем пример подтверждения только 1-го характеристики. Докажем, к примеру, свойство 3.
Пусть для А=(аij
), B=(bij
), C=(cij
) произведения матриц определены. Найдем элемент i-ой строчки и j-го столбца матрицы А(В+С). Это будет число
аi
1
(b1
j
+c1
j
)+ аi
2
(b2
j
+c2
j
)+…+аin
(bnj
+cnj
) =
(аi
1
b1
j
+ai
2
b2
j
+…+ain
bnj
)+ (аi
1
c1
j
+ai
2
c2
j
+…+ain
cnj
).
1-ая сумма в правой части равенства равна элементу из i-ой строчки и j-го столбца матрицы АВ, а 2-ая сумма равна элементу из i-ой строчки и j-го столбца матрицы АС. Рассуждение правильно при всех i и j, то свойство 3 подтверждено.
Упражнение 1. Проверьте свойство ассоциативности 1 для матриц:
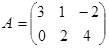 ,
, 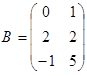 ,
, 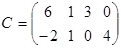 .
.
Упражнение 2. Проверьте свойство дистрибутивности 2 для матриц:
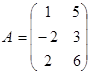 ,
, 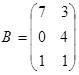 ,
, 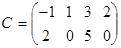 .
.
Упражнение 3. Отыскать матрицу А3
, если 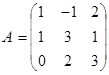 .
.
Вырожденные и невырожденные матрицы
Определение. Матрица именуется вырожденной, если ее определитель равен нулю, и невырожденной, если определитель матрицы отличен от нуля.
Пример. 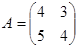 ,
, 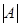 = 16-15 = 1
= 16-15 = 1 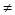 0; А – невырожденная матрица.
0; А – невырожденная матрица.
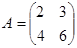 ,
, 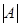 = 12-12 = 0; А – вырожденная матрица.
= 12-12 = 0; А – вырожденная матрица.
Аксиома. Произведение матриц есть вырожденная матрица и тогда лишь тогда, когда хотя бы один из множителей есть вырожденная матрица.
Необходимость. Пусть АВ – вырожденная матрица, т.е. 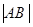 =0. Тогда, в силу того, что определитель произведения матриц равен произведению определителей перемножаемых матриц, имеем
=0. Тогда, в силу того, что определитель произведения матриц равен произведению определителей перемножаемых матриц, имеем 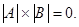 Это означает, что хотя бы одна из матриц А либо В является вырожденной.
Это означает, что хотя бы одна из матриц А либо В является вырожденной.
Достаточность. Пусть в произведении АВ матрица А вырожденная, т.е. 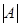 =0. Найдем
=0. Найдем 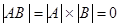 , т.к.
, т.к. 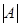 =0; итак,
=0; итак, 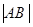 =0; АВ — вырожденная матрица.
=0; АВ — вырожденная матрица.
Замечание. Доказанная аксиома справедлива для хоть какого числа множителей.
Оборотная матрица
Определение. Квадратная матрица В именуется оборотной по отношению к матрице А такового же размера, если
АВ = ВА = Е. (1)
Пример. 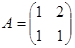 ,
, 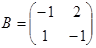 .
.
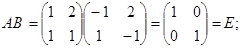
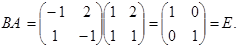
В – матрица оборотная к А.
Аксиома. Если для данной матрицы оборотная существует, то она определяется совершенно точно.
Представим, что для матрицы А есть матрицы Х и У, такие, что
АХ = ХА = Е (2)
АУ = УА = Е (3)
Умножая одно из равенств, к примеру, АХ = Е слева на У, получим У(АХ) = УЕ. В силу ассоциативности умножения имеем (УА)Х = УЕ. Так как УА = Е, то ЕХ = УЕ, т.е. Х = У. Аксиома подтверждена.
Аксиома (нужное и достаточное условие существования оборотной матрицы).
Оборотная матрица А-1
существует и тогда лишь тогда, когда начальная матрица А невырожденная.
Необходимость. Пусть для матрицы А существует оборотная А-1
, т.е. А 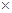 А-1
А-1
= А-1
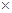 А = Е. Тогда, ½А
А = Е. Тогда, ½А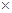 А-1
А-1
½= ½А½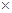 ½А-1
½А-1
½=½Е½=1, т.е. ½А½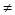 0 и ½А-1
0 и ½А-1
½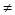 0; А – невырожденная.
0; А – невырожденная.
Достаточность. Пусть дана невырожденная матрица порядка n
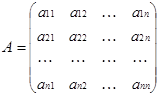 ,
,
так что ее определитель 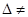 0. Разгляди матрицу, составленную из алгебраических дополнений к элементам матрицы А:
0. Разгляди матрицу, составленную из алгебраических дополнений к элементам матрицы А:
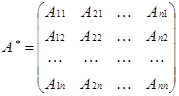 ,
,
ее именуют присоединенной к матрице А.
Следует направить внимание на то, что алгебраические дополнения к элементам i-ой строчки матрицы А стоят в i-ом столбце матрицы А*
, для 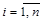 .
.

 Найдем произведения матриц АА*
Найдем произведения матриц АА*
и А*
А. Обозначим АА*
через С, тогда по определению произведения матриц имеем: Сij
= аi
1
А 1
j
+ аi
2
А 2
j
+ … + аin
Аnj
; i = 1, n: j = 1, n.
При i = j получим сумму произведений частей i — ой строчки на алгебраические дополнения данной же строчки, таковая сумма приравнивается значению определителя. Таковым образом Сij
= |А| = D — это элементы главной диагонали матрицы С. При i j, т.е. для частей Сij
j, т.е. для частей Сij
вне главной диагонали матрицы С, имеем сумму произведений всех частей некой строчки на алгебраические дополнения иной строчки, таковая сумма приравнивается нулю. Итак,  = АА*
= АА*
Аналогично доказывается, что произведение А на А*
равно той же матрице С. Таковым образом, имеем А*
А = АА*
= С. Отсюда следует, что
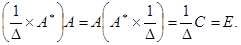
Потому, если в качестве оборотной матрицы взять 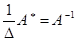 , то
, то 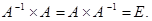 Итак, оборотная матрица существует и имеет вид:
Итак, оборотная матрица существует и имеет вид:
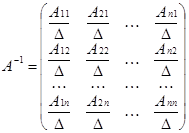 .
.
Пример. Найдем матрицу, оборотную к данной:
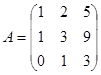
Находим D = |А| = -1 ¹ 0, А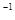 существует. Дальше находим алгебраические дополнения частей матрицы А:
существует. Дальше находим алгебраические дополнения частей матрицы А:
А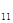 =
= 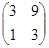 = 0 ; А
= 0 ; А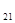 =
= 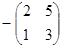 = -1; А
= -1; А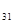 =
= 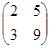 = 3;
= 3;
А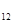 =
= 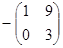 = -3; А
= -3; А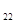 =
= 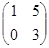 = 3; А
= 3; А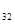 =
= 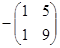 = -4;
= -4;
А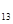 =
= 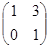 = 1; А
= 1; А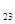 =
= 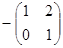 = -1; А
= -1; А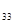 =
= 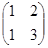 = 1;
= 1;
А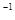 =
= 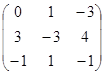
]]>

 (5 оценок, среднее: 4,80 из 5)
(5 оценок, среднее: 4,80 из 5)