Учебная работа. Реферат: История становления и развития математического моделирова-ния

Учебная работа. Реферат: История становления и развития математического моделирова-ния

История становления и развития математического моделирования

Реферат по курсу математического моделирования ст. Ильиных А.А.

Новосибирский Муниципальный технический Институт

Кафедра ТЭС

Новосибирск 2002 г.

Введение.

В век веба и галлактических технологий тяжело представить инженера-разработчика без компа. Современные исследования так наукоёмки, что просто на физическом уровне нереально обойтись без помощи вычислительной машинки. Колоссальные объёмы инфы требуется рассматривать в процессе исследования действий в разных областях науки и техники. В теплоэнергетике исследуются различные процессы горения горючего в разных моделях топок, процессы течения парожидкостных консистенций в проточных частях турбогенераторов (расчёт нагрева сплава и его расширение при разных граничных критериях, основывается на решении уравнений теплопроводимости) и расплавленных металлов, являющихся теплоносителем первого контура, в парогенераторах атомных электронных станций, исследуется воздействие струй пара на поверхность лопаток турбины, что нужно для предотвращения их коррозионного износа, так же исследуются процессы протекания ядерных реакций в тепловыделяющих элементах ( ТВЭЛах ) и т.д. и т.п. По сути большая часть действий в теплоэнергетике уже издавна исследовано. Исследования проходят по оптимизации этих действий и исследованию глубинной сущности явлений для заслуги наибольшего эффекта при разработке энергетического оборудования. тут и нужна математическая модель. Совершенно математическое моделирование появилось с появлением вычислительной техники. Это обосновано потребностью человека в разных областях. Население земли просит удобства. Конкретно для нужд возрастающего населения Земли нужно развитие науки и техники (исследования вселенной, исследование протекающих в земной коре действий, прогнозирование землетрясений, прогнозирование погоды, исследования глобальных конфигураций атмосферного климата, электроника, наземный, аква, подводный экологически незапятнанный транспорт, аэродинамика, внедрения новейших экозащитных технологий, разработка новейших материалов и т.д.). Становление математического моделирования проходило с развитием индустрии, научного познания и что греха таить является детищем гонки вооружений меж странами. Конкретно военные изобрели веб и конкретно они обширно употребляют моделирование (начиная от бактериологического орудия и заканчивая моделированием ядерных, атомных, термоядерных взрывов на суперкомпьютерах). Исследования по механике воды и газа на базе уравнений Навье Стокса имеют в нашей стране давнешние традиции. Начало им положено ещё в первой половине 60-х годов в трудах участников семинара НИИ (Научно-исследовательский институт — самостоятельное учреждение, специально созданное для организации научных исследований и проведения опытно-конструкторских разработок) ВЦ МГУ (Московский государственный университет имени М. В. Ломоносова) по численным способам аэромеханики, работавшего под управлением Г.И. Петрова, Л.А. Чудова, Г.Ф. Теленина, Г.С. Рослякова. Эти работы удачно развивались благодаря удачным достижениям русских учёных в вычислительной арифметике. Посреди почти всех рассматривавшихся в то время классов задач гидро- и аэродинамики, решение которых не могло быть получено в рамках теории пограничного слоя либо невязкого газа (отрывные течения, взаимодействие ударной волны и пограничного слоя, структура ударной волны и т.д.), в работах В.И. Полежаева было существенно продвинуто исследование естественно-конвективных действий. Действенные численные способы и программки, разработанные для этого класса задач, дозволили уже на ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач) второго поколения решить почти все фактически принципиальные задачки (исследование эффективности термический изоляции, термообмен и температурное расслоение при хранении воды в сосудах, конвекция в глубочайшей атмосфере для интерпретации данных зондирования атмосферы Венеры, исследование гидромеханики невесомости и анализ результатов технологических тестов в мироздании), также изучить структуру нелинейных конвективных течений.

К истинному времени становится всё наиболее ясным, что все трудности, возникающие в аэро- и гидродинамике при численном решении уравнений Навье Стокса, навряд ли будут решены даже на ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач) с сотками млрд операций в секунду. Задачки конвекции в замкнутых плоских областях и сосудах, которые были исторически первыми для математического моделирования на базе уравнений Навье Стокса, стали уже издавна традиционными. Для этого класса задач (либо для так именуемых моделей общего предназначения) создателями установлены фундаментальные закономерности, к числу которых относится эффект максимума температурного (концентрационного) расслоения.

Благодаря достигнутому в работе высочайшему уровню открываются перспективы широкого внедрения методологии и определенных физических результатов в рассматриваемых направлениях, также пути наиболее действенного внедрения способов математического моделирования с внедрением современной вычислительной техники в разных предметных областях.

Основная часть.

Главные соответствующие черты моделирования.

Проникновение математических способов в самые различные, тотчас нежданные сферы людской деятель значит возможность воспользоваться новенькими, как правило, очень плодотворными средствами исследования. Рост математической культуры профессионалов в соответственных областях приводит к тому, что исследование общих теоретических положений и способов вычислений уже не встречает серьёзных проблем. вкупе с тем на практике оказывается, что одних только математических знаний далековато не довольно для решения той либо другой прикладной задачки – нужно ещё получить способности в переводе начальной формулировки задачки на математический язык. В этом и состоит неувязка овладения искусством математического моделирования.

Холл (1963) произнес, что целью прикладной арифметики является математическое осмысление реальности. С иной стороны, инжинеру-практику, пожалуй, наиболее принципиально знать, выдержит ли его мост предполагаемую нагрузку, хватит ли закупленного угля до конца отопительного сезона и не лопнет ли лопатка в турбине, — другими словами, получить определенные ответы на определенные вопросцы. В практике математического моделирования начальным пт нередко является некая эмпирическая ситуация, выдвигающая перед исследователем задачку, на которую требуется отыскать ответ. До этого всего, нужно установить, в чём конкретно заключается задачка. Нередко (но не постоянно) наряду с данной стадией постановки задачки идет процесс выявления главных либо существенных особенностей явления (рис. 1). А именно для физических явлений этот процесс схематизации либо идеализации играет решающую роль так как в настоящем явлении участвует огромное количество действий и оно очень трудно. Некие черты явления представляются необходимыми почти все остальные – несущественными. Возьмём например движение маятника, образованного тяжёлым грузом, подмешанным на конце нити. В этом случае значимым является постоянный нрав колебаний маятника, а несущественным – то, что нить белоснежная, а груз чёрный. Опосля того как значительные причины выявлены, последующий шаг состоит в переводе этих причин на язык математических понятий и величин и постулировании соотношений меж этими величинами. Опосля построения модели её следует подвергнуть проверке. Адекватность модели до некой степени проверяется обычно в процессе постановки задачки. Уравнения либо остальные математические соотношения, сформулированные в модели, повсевременно сопоставляются с начальной ситуацией. Существует несколько качеств проверки адекватности. Во-1-х, сама математическая база модели (которая и составляет её существо) обязана быть непротиворечивой и подчиняться всем обыденным законам математической логики. Во-2-х, справедливость модели зависит от её возможности правильно обрисовывать начальную ситуацию. Модель можно вынудить отражать реальность, но она не есть сама реальность.

Набросок 1.

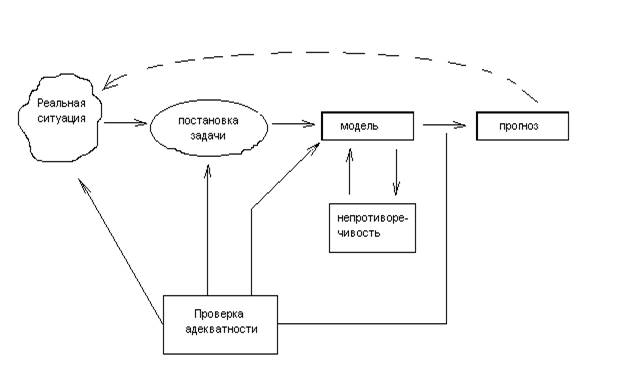
Ситуации моделируют для различных целей. Основная из их – необходимость предвещать новейшие результаты либо новейшие характеристики явления. Эти пророчества могут быть соединены с распространением имеющихся результатов либо иметь наиболее принципный нрав. Нередко они относятся к условиям, которые, по всей вероятности, будут иметь пространство в некий момент в дальнейшем. С иной стороны, пророчества могут относится к событиям, конкретное экспериментальное исследование которых невыполнимо. Более принципиальный пример такового рода дают бессчетные прогнозы, которые делались на базе математических моделей в программке галлактических исследовательских работ. Но для данной цели моделируются не все ситуации: в неких вариантах довольно уметь обрисовывать математическими средствами работу системы для того, чтоб достигнуть наиболее глубочайшего осознания явления (конкретно эту роль и играют почти все выдающиеся физические теории, хотя на их базе делаются также и прогнозы). Обычно при таком математическом описании не учитывается элемент контроля, но в моделях, построенных, к примеру, для исследования работы сетей, таковых как схемы движения поездов либо самолётов, контроль нередко является принципиальным фактором.

Математическая модель представляет собой упрощение настоящей ситуации. Осязаемое упрощение наступает тогда, когда несущественные индивидуальности ситуации отбрасываются и непростая начальная задачка сводится к идеализированной задачке, поддающейся математическому анализу. Конкретно при таком подходе в традиционной прикладной механике появились блоки без трения, невесомые нерастяжимые нити, невязкие воды, полностью твёрдые либо чёрные тела и остальные подобные идеализированные модели. Эти понятия не есть в настоящей реальности, они являются абстракциями, составной частью идеализации, предпринятой создателем модели. И тем не наименее их нередко можно с фуррором считать неплохим приближением к настоящим ситуациям. Описанный образ действий при построении математических моделей не является единственным, и этому совершенно не стоит удивляться. В другом вероятном подходе первым шагом является построение обычной модели нескольких более соответствующих особенностей явления. Это нередко делается для того, чтоб ощутить данную задачку, причём делается это ещё до того, как сама задачка совсем сформулирована. Потом эта модель обобщается, чтоб охватить остальные факты, пока не будет найдено применимое либо адекватное решение. Есть ещё подход, когда с самого начала вводится в рассмотрение сразу огромное число причин. Он нередко применяется в исследовании операций, и такие модели обычно изучают имитационными способами с внедрением ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач).

Важное решение, которое нередко принимается в самом начале процесса моделирования, касается природы рассматриваемых математических переменных. По существу они делятся на два класса. В один из их входят известные свойства, т.е. величины, поддающиеся (по последней мере на теоретическом уровне) четкому измерению и управлению. Такие переменные именуются детерминированными переменными. В иной класс входят неведомые свойства, т.е. величины, которые никогда не могут быть буквально измерены и имеют случайный нрав – они именуются стохастическими переменными. Модель, содержащая стохастические переменные, обязана по определению описываться математическим аппаратом теории вероятностей и статистики. Детерминированные переменные нередко, но не постоянно требуют вербования обыденного математического анализа. Природа неких ситуаций бывает ясна не сходу, остальные ситуации характеризуются переменными обоих типов. Для построения модели очень принципиально, чтоб природа переменных была верно представлена.

2. Эволюционный процесс в моделировании.

Говоря о математическом моделировании, недозволено не направить внимания на эволюционный процесс «смены» парадигм моделирования, который, как кажется, характерен для почти всех дисциплинарных областей, где используются способы теории управления. До сего времени ни в одной из работ по теории моделирования этот процесс не рассматривался как «смена поколений» математических моделей. Тем не наименее, на данный момент можно было бы гласить уже о 3-х таковых поколениях. На первых шагах речь почаще всего идет о математической записи отдельных феноменологических наблюдений над настоящими объектами. Для их свойственна простота описаний, типична линейность уравнений и малая размерность (нередко воспроизводится всего одна либо две переменных). Способы анализа соединены в главном с получением аналитических решений и графическим рассмотрением на фазовой плоскости. Потом возникают модели, описывающие объект «во всей его полноте» — в их объект представлен в виде «системы» — модель отражает его структуру и законы, по которым он работает. Модели стают значительно нелинейными, чисто математический аппарат дополняется логико-семантическим. Увеличивается размерность, достигая нескольких 10-ов. Такие модели именуются «сложными», «большенными», а рабочим инвентарем на этом шаге становится вычислительный время начинается переход к третьему поколению математических моделей — моделям виртуального мира. виртуальное моделирование можно найти как проигрывание трехмерного мира компьютерными средствами. Резко растет размер обрабатываемой и воспроизводимой инфы (к примеру, количество визуализируемых «деталей» добивается нескольких тыщ). Интересно, что модели третьего поколения по собственной математической сути могут быть как «феноменологическими», так и «системными» — на содержании этих понятий мы остановимся чуток ниже.

процесс смены поколений моделей можно проиллюстрировать на почти всех дисциплинарных примерах — в небесной механике это переход от феноменологической модели Птолемея к системной модели Коперника-Кеплера и потом к современным моделям (таковым, как совокупные модели движения объектов в галлактическом пространстве в системах слежения, применяемых в астронавтике и в военном деле, либо как виртуальные модели небесных явлений в мультимедийных системах Redshift).

В биомедицине 1-ое поколение моделей возникло в самом конце XIX в. — модель сердца как «эластичного резервуара» О.Франка представляла собой типичную феноменологическую модель (модель данных). Бессчетные модели физиологических действий охарактеризовали приход второго поколения моделей — системных моделей действий жизнедеятельности, использовавшихся для исследования действий управления искусственными органами. Развитие тренажерных моделей (в том числе мультимедийных) охарактеризовывает начало третьего шага.

В конце концов, таковая же картина наблюдается в управлении технологическими действиями. Феноменологические модели передаточных функций, восстановленные по входо-выходным чертам объектов, сменились системными способами места состояний. 3-ий шаг математического моделирования также связан тут с виртуальным моделированием — динамическим моделированием в настоящем масштабе времени.

Говоря о Рф, можно вспомянуть, что наука математического моделирования развивается с 1960-х гг. и имеет огромные традиции. Но для нас на данный момент принципиально другое — часть скопленного тогда потенциала, получившая развитие в теории управления и ее применениях, до сего времени остается «невостребованной» современной наукой о моделировании в ее «чистом» виде, оставшись и за рамками книжки.

Отметим, что почти все фундаментальные трудности прикладного моделирования в первый раз были выявлены И.А.Полетаевым. Он первым направил внимание на утилитарность математических моделей, дав необычную систематизацию моделей по целям их использования: «поисковая» модель — для проверки гипотез, «портретная», она же — демо, — для подмены объекта в опыте (к примеру, для тренажеров — что в то время рассматривалось чуть ли не как научная фантастика) и, в конце концов, «экспериментальная модель», что в современном осознании значит ориентацию на непростой вычислительный один настолько же принципиальный круг вопросцев — о принципной «субъективности» математического моделирования. По наименьшей мере два его выражения и сейчас заслуживают внимания:

В задачке математического моделирования <<не считая объекта моделирования и модели, непременно находится субъект моделирования, лицо, усилиями и в интересах которого осуществляется модель>>. Роль субъекта моделирования оказывается решающей, ибо конкретно его цели, интересы и предпочтения сформировывают модель.

Создание модели необходимо не {само по себе}, а для решения практических задач, что лишь и может оправдать затрату сил на создание модели. Модель создается для того, чтоб работать: <<Лишь полная реализация модели с ее «прогоном» через расчеты вполне оправдывает Издержки на моделирование>>.

к примеру, проведение экспериментальных исследовательских работ на больших высокотемпературных агрегатах соединено с большенными организационными и техническими трудностями. Потому возникает необходимость в разработке математических моделей, существенно сокращающих объём трудоёмких и дорогостоящих промышленных тестов, на долю которых остаётся только сбор начальной инфы для расчёта, проверка адекватности математических моделей и внедрение результатов моделирования. Для формулировки граничных критерий нужен детализированный расчёт наружного термообмена. Одним из более распространённых способов расчёта наружного термообмена является зональный способ, рассматривающий перенос тепла излучением, конвекцией и турбулентной теплопроводимостью, т.е. учитывающий неравномерность распределения температур, скоростей и концентраций в рабочем пространстве топки.

]]>