Учебная работа. Реферат: К вопросу о «высокотемпературных» осцилляциях магнетосопротивления висмута в ультраквантовом пределе

Учебная работа. Реферат: К вопросу о «высокотемпературных» осцилляциях магнетосопротивления висмута в ультраквантовом пределе

К вопросцу о «высокотемпературных» осцилляциях магнетосопротивления висмута в ультраквантовом пределе

д. ф.-м. н. Богод Ю.А.

Проанализированы характеристики «высокотемпературных» осцилляций магнетосопротивления висмута в ультраквантовом пределе. Имеющиеся экспериментальные результаты несовместимы с физической моделью [22-24] и описываются при помощи модели [20,21].

«Высокотемпературные» осцилляции (ВТО) в первый раз наблюдались в 1973г. [1] при исследовании магнетосопротивления висмута. одной из отличительных особенностей, послужившей предпосылкой выбора наименования эффекта, является слабенькое температурное затухание амплитуды осцилляций, что делает вероятным их наблюдение в спектре от 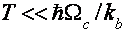до 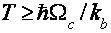( 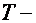температура, 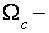циклотронная частота, 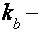неизменная Больцмана). Период ВТО в оборотном магнитном поле приблизительно в 2-2.5 раза меньше периода осцилляций Шубникова-де Газа, и не зависит от ферми-энергии .

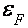К истинному времени ВТО детально исследованы в монокристаллах Bi высочайшей чистоты, монокристаллических сплавах 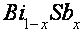, также в сплавах с донорными и акцепторными примесями (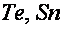) [2-11]. Не считая того, изучались ВТО термоэдс [12,13], воздействие на характеристики осцилляций магнетосопротивления всестороннего сжатия и одноосных деформаций [14,15], роль мощного магнитного поля [5, 16-19].

Есть две другие модели, в каких изготовлена попытка обрисовать характеристики ВТО. Согласно первой из их [20,21] предпосылкой появления ВТО являются электрон-дырочные переходы у границ энергетических зон. Возможность таковых переходов связана с тем обстоятельством, что в висмуте даже при низких температурах число занятых состояний носителей заряда над ферми-уровнем (поблизости границ примыкающих зон) добивается 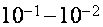и определяется уширением энергетических уровней, обусловленным релаксационными действиями [21]. В рассматриваемой модели период ВТО в случае квадратичного закона дисперсии связан с энергией перекрытия 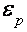, равной сумме ферми-энергий электронов и дырок 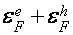, и циклотронной массой носителей заряда.

В работах [22-24] предложена модель, согласно которой осцилляции появляются в итоге электрон-дырочных переходов меж экстремумами подзон Ландау поблизости ферми-уровня. При всем этом циклотронные массы электронов и дырок должны быть кратны. В модификации данной модели [25] период осцилляций определяется комбинированной площадью 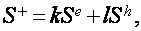где 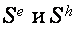— площади экстремальных сечений электрической и дырочной ферми-поверхностей, а отношение 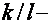целое число, равное отношению циклотронных масс дырок и электронов.

Тестом при выбирании модели могут служить характеристики висмута в ультраквантовом пределе: согласно [22-24] в этих критериях ВТО исчезают вкупе с осцилляциями Шубникова-де Гааза, а по [20,21] в ультраквантовом пределе ВТО продолжают наблюдаться. Ниже экспериментальные результаты, приобретенные в мощных магнитных полях, дискуссируются с данных позиций.

1.Магнитное поле параллельно биссекторной оси (Н||
C
1).

В данных критериях реализуются экстремальные сечения электрических ферми-поверхностей с циклотронными массами 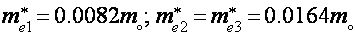(легкие электроны), и экстремальное сечение дырочной ферми-поверхности с циклотронной массой 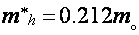(томные дырки). Отношение спинового и орбитального расщеплений для электронов 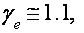для дырок 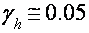[26-29]. В районе 25 кэ электроны перебегают в ультраквантовый предел [29-30]. Согласно данным работ [5,17] (в каких опыты проводились при помощи различных методик) ВТО продолжают наблюдаться прямо до 56-60 кэ- наибольших магнитных полей в цитируемых работах. наблюдение ВТО в ультраквантовом пределе противоречит разъяснению их происхождения в рамках рассмотрения [23-25] и согласуется с моделью [20,21].

2. Магнитное поле параллельно бинарной оси (Н||
C
2).

В данной для нас геометрии наблюдаются легкие электроны ( 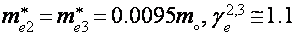), томные электроны (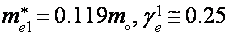) и томные дырки (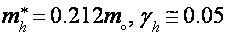). В магнитном поле, большем 15 кэ, легкие электроны перебегают в ультраквантовый предел [29-30,18]. Дальше, в магнитном поле Н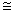120 кэ дно зоны томных электронов пересекает ферми-уровень (исчезают электрические осцилляции Шубникова-де Газа). В работе [18] сообщается о наблюдении при Н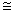111 кэ крайнего экстремума ВТО, что также связывается с пересечением дна электрической зоны и ферми-уровня. Данное событие создатель работы [25] разглядывает как доказательство физической модели ВТО, предложенной в [22-24]. Но данной для нас модели противоречит некратность циклотронных масс томных электронов и дырок для данного направления Н.

3. Магнитное поле параллельно тригональной оси (Н||
C
3).

При данной ориентации Н наблюдаются близкие циклотронные массы электронов и дырок 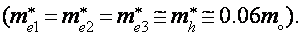Для соотношений спинового и орбитального расщеплений имеем 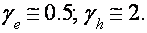В магнитном поле 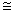100 кэ дырки перебегают в ультраквантовый предел [30,19], и это сопровождается исчезновением ВТО [19]. Исчезновение осцилляций Шубникова-де Газа и ВТО при близких значениях магнитного поля связывается [19] с представлениями [22-24].

Таковым образом, в ультраквантовом пределе ситуация с выбором модели для описания ВТО очевидно разнопланова. Делая упор на то, что при Н||C1 приобретенные данные несовместимы с рассмотрением [22-25], проанализируем результаты при Н||C2 и Н||C3 в рамках модели [20,21] с учетом зонной структуры висмута. Так как угловая зависимость периода ВТО в целом подобна угловой зависимости дырочных циклотронных масс [4,6,13], мы ограничимся рассмотрением дырочных осцилляций. До этого всего напомним, что, согласно [20], ВТО при квазиупругом междолинном рассеянии в простейшом случае можно обрисовать соотношением

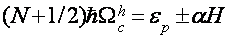, (1)

где крайнее слагаемое соединено со смещением края электрической зоны. В согласовании с (1), всякий раз, когда экстремум подзоны Ландау дырочной ветки диапазона оказывается у дна зоны проводимости, частота столкновений испытывает скачок, связанный с воззванием в нуль числа состояний электрической ветки диапазона ниже дна зоны проводимости, т.е. появляются осцилляции кинетических коэффициентов с периодом [21,2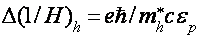2]

(2)

При неупругом межзонном рассеянии на акустических фононах с энергией 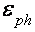возникает наложение мод с периодами

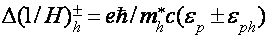(3)

При помощи соотношений (2), (3) были получены усредненные значения энергии перекрытия зон 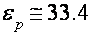мэв и энергии «межзонных» акустических фононов 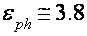мэв. 1-ое из их соответствует 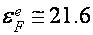мэв, что согласуется с более достоверной величиной ферми-энергии электронов, приведенной в обзоре [29]. Энергия «межзонных» акустических фононов соответствует данным [31].

Уже говорилось, что в случае Н||C2 реализуются легкие и томные электроны с значительно разными величинами спинового расщепления уровней Ландау (см. выше). Дно зоны томных электронов 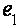с ростом магнитного поля довольно стремительно сдвигается ввысь по энергии, а дно каждой зоны легких электронов ( 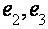) стремительно сдвигается вниз по энергии. Соответственно, заселенность дырочных состояний на уровне дна зоны электронов 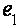вырастает в меру уменьшения разности ферми-энергии и энергии дна зоны [21]. ясно, что в таковой ситуации в довольно сильном магнитном поле определяющий вклад в амплитуду ВТО будут заносить дырочные переходы в зону томных электронов. При пересечении дна зоны 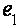и ферми-уровня амплитуда ВТО обязана резко уменьшиться по последней мере на порядок, будучи связанной только с дырочными переходами в зоны легких электронов, нулевые уровни энергии которых удалены от ферми-уровня на расстояние ~10 мэв. Может быть, что регистрация этих «остаточных» осцилляций в реализуемых [18] экспериментальных критериях проблематична.

В магнитном поле, параллельном тригональной оси, когда спиновое расщепление уровней Ландау дырок в два раза превосходит орбитальное, конкретно опосля момента пересечения подзоной Ландау дырок 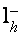ферми-уровня дырок 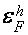дырочные состояния оказываются сосредоточенными поблизости экстремума подзоны Ландау 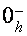(рис.1), выше начального потолка валентной зоны на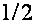 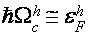. Можно считать, что сейчас число занятых дырочных состояний на уровне дна электрической зоны значительно уменьшится. Для иллюстрации этого происшествия оценим относительное число дырочных состояний поблизости ферми-уровня при 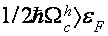, которое по порядку величины есть 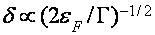(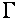— уширение экстремума 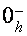). В согласовании с известными значениями частот столкновений носителей заряда в висмуте [29,32-33] примем 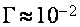мэв, что дает 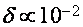. Уменьшение числа дырочных состояний на уровне дна электрической зоны равносильно резкому уменьшению числа приграничных межзонных переходов. Другими словами, при пересечении подзоной Ландау дырок 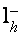ферми-уровня, сразу с исчезновением дырочных осцилляций Шубникова-де Газа скачком приблизительно на два порядка миниатюризируется амплитуда дырочных ВТО. Крайний перед скачком экстремум ВТО, соответственный сближению уровне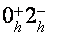й и 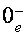(рис.1), должен реализоваться в магнитном поле 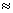96 кэ, определяемом из соотношения

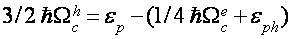(4)

Расчетное

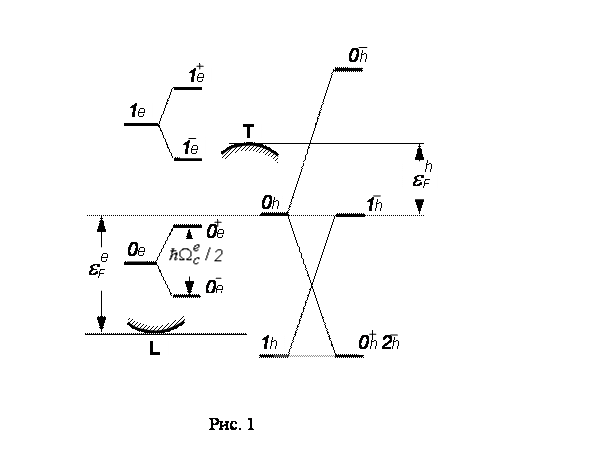
Фрагмент зонной структуры висмута в магнитном поле, параллельном тригональной оси, порог ультраквантового предела. Штриховкой выделены зонные экстремумы при Н=0.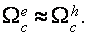

Таковым образом, совокупа параметров ВТО в ультраквантовом пределе быть может верифицирована в рамках модели [20,21].

Перечень литературы

1. Ю.А. Богод, Вит.Б. Красовицкий, Препринт ФТИНТ АН УССР (1973)

2. Ю.А. Богод, Вит.Б Красовицкий, В.Г. Герасимечко, ЖЭТФ 66, 1362 (1974)

3. Ю.А. Богод, Вит.Б. Красовицкий, В.Г. Герасимечко, ФТТ 17, 1799 (1975)

4. Ю.А. Богод, В.Г. Герасимечко, Вит.Б. Красовицкий, ФНТ 1, 1472 (1975)

5. Ю.А. Богод, Вит.Б. Красовицкий, Письма в ЖЭТФ 24, 585 (1976)

6. Ю.А. Богод, Вит.Б. Красовицкий, С.А. Миронов, ЖЭТФ 78, 1099 (1980)

7. Ю.А. Богод, Вит.Б. Красовицкий, Е.Т. Лемешевская, ФНТ 7, 1530 (1981)

8. Ю.А. Богод, Вит.Б. Красовицкий, Е.Т. Лемешевская, ФНТ 9, 34 (1983)

9. Ю.А. Богод, Вит.Б. Красовицкий, Е.Т. Лемешевская, ФНТ 9, 832 (1983)

10. Ю.А. Богод, Вит.Б. Красовицкий, Е.Т. Лемешевская, ФНТ 12, 610 (1986)

11. Ю.А. Богод, Вит.Б. Красовицкий, ФНТ 16, 900 (1990)

12. Ю.А. Богод, Вит.Б. Красовицкий, Е.Т. Лемешевская, ФНТ 12, 435 (1986)

13. Ю.А. Богод, Вит.Б. Красовицкий, В.Я. Левантовский, Е.Т. Лемешевская, ФНТ 14, 1252 (1988)

14. А.Г. Бударин, В.А. Вентцель, А.В. Руднев, Ю.А. Богод, Вит.Б. Красовицкий, ФНТ 14, 875 (1988)

15. Вит.Б. Красовицкий, В.В. Хоткевич, ФНТ 17, 710 (1991)

16. Yu.A. Bogod and A. Libinson, Solid State Commun. 96, 609 (1995)

17. Yu.A. Bogod and A. Libinson, Phys. Status Solidi B197, 137 (1996)

18. Вит.Б. Красовицкий, В.В. Хоткевич, А.Г. Янсен, П. Видер, ФНТ 25, 903 (1999)

19. V.B. Krasovitsky, International J.of Modern Physics B16, 3054 (2002)

20. Ю.А. Богод, ФНТ 12, 1004 (1986)

21. Ю.А. Богод, Л.Ю. Горелик, А.А. Слуцкин, ФНТ 13, 626 (1987)

22. В.М. Поляновский, Письма в ЖЭТФ 46, 108 (1987)

23. В.М. Поляновский, УФЖ 33, 1575 (1988)

24. В.М. Поляновский, УФЖ 34, 459 (1989)

25. Ю.Ф. Комник, ФНТ 29, 1231 (2003)

26. Yi-HanKao, Phys.Rev. 129, 1122 (1963)

27. R.J. Dinger, and A.W. Lawson, Phys.Rev. B7, 5215 (1973)

28. В.С. Эдельман, М.С. Хайкин, ЖЭТФ 49, 405 (1965)

29. В.С. Эдельман, УФН 123,257 (1977)

30. G.E. Smith, G.A. Baraff and J.R. Rowell, Phys.Rev. 135A, 1118 (1964)

31. A.A. Lopez, Phys.Rev. 175, 823 (1968)

32. R.H. Hartmann, Phys.Rev 181, 1070 (1969)

33. M.P. Vecci, J.P. Pereira and M.S. Dresselhaus, Phys.Rev. B14, 298 (1976)

]]>