(8 оценок, среднее: 4,75 из 5)
Загрузка...
Учебная работа. Реферат: Мир глазами Поля Дирака: объединение идей квантовой механики и релятивизма
По собственному построению квантовая механика является значительно нерелятивистской теорией: применяемое в уравнении Шредингера выражение для оператора Гамильтона является обобщением традиционной формулы для энергии. Для огромного количества настоящих приложений теории (физика кристаллов, химия, биология) требование малости скоростей не является значимым ограничением: спектр энергий, с которыми приходится иметь дело в земных критериях недостаточен для разгона объектов до релятивистских скоростей. Но существует целый ряд разделов естествознания, развитие которых сделало животрепещущим вопросец о разработке релятивистской квантовой теории. К ним до этого всего следует отнести разделы физики, специализирующиеся взаимодействием света с веществом: зародившаяся в итоге попыток осознать физическую природу света квантовая механика оказалась неспособной правильно обрисовать ультрарелятивистскую частичку — фотон. Релятивистская теория микромира нужна физике ядра и простых частиц, так как изучаемые в ее рамках процессы с ролью мощных взаимодействий сопровождаются обменом большенными порциями энергии, что безизбежно соединено с появлением больших скоростей. Космологические теории эволюции Вселенной и Огромного Взрыва требуют развития аппарата описания вещества в экстремальных (с нашей точки зрения) состояниях. В конце концов, наличие плохо связанных вместе релятивистской и квантовой теорий, любая из которых по-своему “разъясняла” традиционную теорию, являющуюся предельным случаем каждой из их, безизбежно ставило вопросец о их объединении. Пробы обобщения квантовой механики и придания ей релятивистски инвариантной формы делались практически с первых шагов ее сотворения, но до сего времени еще не привели к созданию законченной и стопроцентно вольной от внутренних противоречий теории.
S-матрица. Доборной сложностью, присущей релятивистской теории является несохранение числа частиц, участвующих в процессе. А именно это значит, что неважно какая рассматриваемая система подабающая владеть нескончаемым числом степеней свободы. Так как сама процедура измерения координат частички в принципе может приводить к рождению новейших частиц, она становится принципно глупой. Релятивистская квантовая теория отрешается не только лишь от описания пространственного положения микрообъектов, да и от описания действий с их ролью в виде происходящих поочередно (друг за другом) промежных событий. Расчеты поддаются только амплитуды вероятностей переходов системы из начального состояния при 
, в каком все входящие в нее частички находятся так далековато друг от друга, что взаимодействие меж ними пренебрежимо не достаточно в одно из допустимых законами сохранения конечное состояние при 
, в каком продукты реакции вновь являются фактически вольными объектами. Набор амплитуд таковых переходов образует s-матрицу, вычисление которой и является задачей релятивистской квантовой теории.
Уравнение Клейна-Гордона было первой успешной попыткой обобщения уравнения Шредингера на вариант релятивистского описания электромагнитных взаимодействий микрообъектов. В базе предложенного вывода лежала мысль поменять нерелятивистский оператор Гамильтона в уравнении Шредингера
на его релятивистский аналог, вид которого устанавливался на основании сопоставления традиционных (не квантово-механических) выражений для релятивистской и нерелятивистской функций Гамильтона:
,
где учтена возможность взаимодействия зарядов с электронным и магнитным полями, описываемыми потенциалами 
и A.
Основная математическая трудность, возникающая при попытке перевести релятивистскую формулу (3) на язык квантово-механических операторов состояла в том, что операция извлечения корня из оператора не определена. Предложенный выход состоял в переходе к уравнению второго порядка, возникающего при возведении в квадрат операторного аналога уравнения (3), где сам оператор Гамильтона согласно (1) заменялся на оператор дифференцирования по времени:
.
Приобретенное таковым образом уравнение могло быть просто протестировано на отлично изученном личном случае описания фотона (q=0, m=0). Подстановка обозначенных значений приводит к обычному уравнению Д’Аламбера, описывающему распространение света в вакууме.
Уравнение Клейна-Гордона в истинное время считается правильным релятивистским обобщением уравнений квантовой механики, не учитывающих наличие спина у микрообъектов. Оно правильно оисывает
По {своему|собственному} построению квантовая механика является {существенно|значительно} нерелятивистской теорией: {используемое|применяемое} в уравнении Шредингера выражение для оператора Гамильтона является обобщением {классической|традиционной} формулы для энергии. Для {множества|огромного количества} {реальных|настоящих} приложений теории (физика кристаллов, химия, биология) требование малости скоростей не является {существенным|значимым} ограничением: {диапазон|спектр} энергий, с которыми приходится иметь дело в земных {условиях|критериях} недостаточен для разгона объектов до релятивистских скоростей. {Однако|Но} существует целый ряд разделов естествознания, развитие которых сделало {актуальным|животрепещущим} {вопрос|вопросец} о разработке релятивистской квантовой теории. К ним {прежде|до этого} всего следует отнести разделы физики, {занимающиеся|специализирующиеся} взаимодействием света с веществом: зародившаяся в {результате|итоге} попыток {понять|осознать} физическую природу света квантовая механика оказалась неспособной {адекватно|правильно} {описать|обрисовать} ультрарелятивистскую {частицу|частичку} — фотон. Релятивистская теория микромира {необходима|нужна} физике ядра и {элементарных|простых} частиц, {поскольку|так как} изучаемые в ее рамках процессы с {участием|ролью} {сильных|мощных} взаимодействий сопровождаются обменом {большими|большенными} порциями энергии, что {неизбежно|безизбежно} {связано|соединено} с {возникновением|появлением} {высоких|больших} скоростей. Космологические теории эволюции Вселенной и {Большого|Огромного} Взрыва требуют развития аппарата описания вещества в экстремальных (с нашей точки зрения) состояниях. {Наконец|В конце концов}, наличие плохо связанных {друг с другом|вместе} релятивистской и квантовой теорий, {каждая|любая} из которых по-своему “{объясняла|разъясняла}” {классическую|традиционную} {концепцию|теорию}, являющуюся предельным случаем каждой из {них|их}, {неизбежно|безизбежно} ставило {вопрос|вопросец} {об|о} их объединении. {Попытки|Пробы} обобщения квантовой механики и придания ей релятивистски инвариантной формы делались {буквально|практически} с первых шагов ее {создания|сотворения}, но {до сих пор|до сего времени} еще не привели к созданию законченной и {полностью|стопроцентно|на сто процентов|вполне} {свободной|вольной} от внутренних противоречий теории.
S-матрица. {Дополнительной|Доборной} сложностью, присущей релятивистской теории является несохранение числа частиц, участвующих в процессе. {В частности|А именно} это {означает|значит}, что {любая|неважно какая} рассматриваемая система {должная|подабающая} {обладать|владеть} {бесконечным|нескончаемым} числом степеней свободы. {Поскольку|Так как} сама процедура измерения координат {частицы|частички} в принципе может приводить к рождению {новых|новейших} частиц, она становится {принципиально|принципно} {бессмысленной|глупой}. Релятивистская квантовая теория {отказывается|отрешается} {не только|не только лишь} от описания пространственного положения микрообъектов, {но и|да и} от описания {процессов|действий} с их {участием|ролью} в виде происходящих {последовательно|поочередно} (друг за другом) {промежуточных|промежных} событий. Расчеты поддаются {лишь|только} амплитуды вероятностей переходов системы из {исходного|начального} состояния при , {в котором|в каком} все входящие в нее {частицы|частички} находятся так {далеко|далековато} друг от друга, что взаимодействие {между|меж} ними пренебрежимо {мало|не достаточно|не много} в одно из допустимых законами сохранения конечное состояние при , {в котором|в каком} продукты реакции вновь являются {практически|фактически} {свободными|вольными} объектами. Набор амплитуд {таких|таковых} переходов образует s-матрицу, вычисление которой и является задачей релятивистской квантовой теории.
Уравнение Клейна-Гордона было первой {удачной|успешной} попыткой обобщения уравнения Шредингера на {случай|вариант} релятивистского описания электромагнитных взаимодействий микрообъектов. В {основе|базе} предложенного вывода лежала {идея|мысль} {заменить|поменять} нерелятивистский оператор Гамильтона в уравнении Шредингера
на его релятивистский аналог, вид которого устанавливался на основании {сравнения|сопоставления} {классических|традиционных} (не квантово-механических) выражений для релятивистской и нерелятивистской функций Гамильтона:
,
где учтена возможность взаимодействия зарядов с {электрическим|электронным} и магнитным полями, описываемыми потенциалами и A.
Основная математическая трудность, возникающая при попытке перевести релятивистскую формулу (3) на язык квантово-механических операторов состояла в том, что операция извлечения корня из оператора не определена. Предложенный выход состоял в переходе к уравнению второго порядка, возникающего при возведении в квадрат операторного аналога уравнения (3), где сам оператор Гамильтона согласно (1) заменялся на оператор дифференцирования по времени:
.
{Полученное|Приобретенное} {таким|таковым} образом уравнение могло быть {легко|просто} протестировано на {хорошо|отлично} изученном {частном|личном} случае описания фотона (q=0, m=0). Подстановка {указанных|обозначенных} значений приводит к {обыкновенному|обычному} уравнению Д’Аламбера, описывающему распространение света в вакууме.
Уравнение Клейна-Гордона в {настоящее|истинное} время считается правильным релятивистским обобщением уравнений квантовой механики, не учитывающих наличие спина у микрообъектов. Оно {адекватно|правильно} оисывает Дефицитность “традиционной” квантовой механики.
По собственному построению квантовая механика является значительно нерелятивистской теорией: применяемое в уравнении Шредингера выражение для оператора Гамильтона является обобщением традиционной формулы для энергии. Для огромного количества настоящих приложений теории (физика кристаллов, химия, биология) требование малости скоростей не является значимым ограничением: спектр энергий, с которыми приходится иметь дело в земных критериях недостаточен для разгона объектов до релятивистских скоростей. Но существует целый ряд разделов естествознания, развитие которых сделало животрепещущим вопросец о разработке релятивистской квантовой теории. К ним до этого всего следует отнести разделы физики, специализирующиеся взаимодействием света с веществом: зародившаяся в итоге попыток осознать физическую природу света квантовая механика оказалась неспособной правильно обрисовать ультрарелятивистскую частичку — фотон. Релятивистская теория микромира нужна физике ядра и простых частиц, так как изучаемые в ее рамках процессы с ролью мощных взаимодействий сопровождаются обменом большенными порциями энергии, что безизбежно соединено с появлением больших скоростей. Космологические теории эволюции Вселенной и Огромного Взрыва требуют развития аппарата описания вещества в экстремальных (с нашей точки зрения) состояниях. В конце концов, наличие плохо связанных вместе релятивистской и квантовой теорий, любая из которых по-своему “разъясняла” традиционную теорию, являющуюся предельным случаем каждой из их, безизбежно ставило вопросец о их объединении. Пробы обобщения квантовой механики и придания ей релятивистски инвариантной формы делались практически с первых шагов ее сотворения, но до сего времени еще не привели к созданию законченной и стопроцентно вольной от внутренних противоречий теории.
S-матрица. Доборной сложностью, присущей релятивистской теории является несохранение числа частиц, участвующих в процессе. А именно это значит, что неважно какая рассматриваемая система подабающая владеть нескончаемым числом степеней свободы. Так как сама процедура измерения координат частички в принципе может приводить к рождению новейших частиц, она становится принципно глупой. Релятивистская квантовая теория отрешается не только лишь от описания пространственного положения микрообъектов, да и от описания действий с их ролью в виде происходящих поочередно (друг за другом) промежных событий. Расчеты поддаются только амплитуды вероятностей переходов системы из начального состояния при , в каком все входящие в нее частички находятся так далековато друг от друга, что взаимодействие меж ними пренебрежимо не достаточно в одно из допустимых законами сохранения конечное состояние при , в каком продукты реакции вновь являются фактически вольными объектами. Набор амплитуд таковых переходов образует s-матрицу, вычисление которой и является задачей релятивистской квантовой теории.
Уравнение Клейна-Гордона было первой успешной попыткой обобщения уравнения Шредингера на вариант релятивистского описания электромагнитных взаимодействий микрообъектов. В базе предложенного вывода лежала мысль поменять нерелятивистский оператор Гамильтона в уравнении Шредингера
на его релятивистский аналог, вид которого устанавливался на основании сопоставления традиционных (не квантово-механических) выражений для релятивистской и нерелятивистской функций Гамильтона:
,
где учтена возможность взаимодействия зарядов с электронным и магнитным полями, описываемыми потенциалами и A.
Основная математическая трудность, возникающая при попытке перевести релятивистскую формулу (3) на язык квантово-механических операторов состояла в том, что операция извлечения корня из оператора не определена. Предложенный выход состоял в переходе к уравнению второго порядка, возникающего при возведении в квадрат операторного аналога уравнения (3), где сам оператор Гамильтона согласно (1) заменялся на оператор дифференцирования по времени:
.
Приобретенное таковым образом уравнение могло быть просто протестировано на отлично изученном личном случае описания фотона (q=0, m=0). Подстановка обозначенных значений приводит к обычному уравнению Д’Аламбера, описывающему распространение света в вакууме.
Уравнение Клейна-Гордона в истинное время считается правильным релятивистским обобщением уравнений квантовой механики, не учитывающих наличие спина у микрообъектов. Оно правильно оисывает Дефицитность “традиционной” квантовой механики.
По собственному построению квантовая механика является значительно нерелятивистской теорией: применяемое в уравнении Шредингера выражение для оператора Гамильтона является обобщением традиционной формулы для энергии. Для огромного количества настоящих приложений теории (физика кристаллов, химия, биология) требование малости скоростей не является значимым ограничением: спектр энергий, с которыми приходится иметь дело в земных критериях недостаточен для разгона объектов до релятивистских скоростей. Но существует целый ряд разделов естествознания, развитие которых сделало животрепещущим вопросец о разработке релятивистской квантовой теории. К ним до этого всего следует отнести разделы физики, специализирующиеся взаимодействием света с веществом: зародившаяся в итоге попыток осознать физическую природу света квантовая механика оказалась неспособной правильно обрисовать ультрарелятивистскую частичку — фотон. Релятивистская теория микромира нужна физике ядра и простых частиц, так как изучаемые в ее рамках процессы с ролью мощных взаимодействий сопровождаются обменом большенными порциями энергии, что безизбежно соединено с появлением больших скоростей. Космологические теории эволюции Вселенной и Огромного Взрыва требуют развития аппарата описания вещества в экстремальных (с нашей точки зрения) состояниях. В конце концов, наличие плохо связанных вместе релятивистской и квантовой теорий, любая из которых по-своему “разъясняла” традиционную теорию, являющуюся предельным случаем каждой из их, безизбежно ставило вопросец о их объединении. Пробы обобщения квантовой механики и придания ей релятивистски инвариантной формы делались практически с первых шагов ее сотворения, но до сего времени еще не привели к созданию законченной и стопроцентно вольной от внутренних противоречий теории.
S-матрица. Доборной сложностью, присущей релятивистской теории является несохранение числа частиц, участвующих в процессе. А именно это значит, что неважно какая рассматриваемая система подабающая владеть нескончаемым числом степеней свободы. Так как сама процедура измерения координат частички в принципе может приводить к рождению новейших частиц, она становится принципно глупой. Релятивистская квантовая теория отрешается не только лишь от описания пространственного положения микрообъектов, да и от описания действий с их ролью в виде происходящих поочередно (друг за другом) промежных событий. Расчеты поддаются только амплитуды вероятностей переходов системы из начального состояния при , в каком все входящие в нее частички находятся так далековато друг от друга, что взаимодействие меж ними пренебрежимо не достаточно в одно из допустимых законами сохранения конечное состояние при , в каком продукты реакции вновь являются фактически вольными объектами. Набор амплитуд таковых переходов образует s-матрицу, вычисление которой и является задачей релятивистской квантовой теории.
Уравнение Клейна-Гордона было первой успешной попыткой обобщения уравнения Шредингера на вариант релятивистского описания электромагнитных взаимодействий микрообъектов. В базе предложенного вывода лежала мысль поменять нерелятивистский оператор Гамильтона в уравнении Шредингера
на его релятивистский аналог, вид которого устанавливался на основании сопоставления традиционных (не квантово-механических) выражений для релятивистской и нерелятивистской функций Гамильтона:
,
где учтена возможность взаимодействия зарядов с электронным и магнитным полями, описываемыми потенциалами и A.
Основная математическая трудность, возникающая при попытке перевести релятивистскую формулу (3) на язык квантово-механических операторов состояла в том, что операция извлечения корня из оператора не определена. Предложенный выход состоял в переходе к уравнению второго порядка, возникающего при возведении в квадрат операторного аналога уравнения (3), где сам оператор Гамильтона согласно (1) заменялся на оператор дифференцирования по времени:
.
Приобретенное таковым образом уравнение могло быть просто протестировано на отлично изученном личном случае описания фотона (q=0, m=0). Подстановка обозначенных значений приводит к обычному уравнению Д’Аламбера, описывающему распространение света в вакууме.
Уравнение Клейна-Гордона в истинное время считается правильным релятивистским обобщением уравнений квантовой механики, не учитывающих наличие спина у микрообъектов. Оно правильно оисывает звериного организма служащая для воплощения контакта с миром вокруг нас В базе поведения лежат потребности звериного организма над которыми надстраиваются исполнительные деяния служащие частиц с нулевым спином.
]]>
По своему построению квантовая механика является существенно нерелятивистской теорией: используемое в уравнении Шредингера выражение для оператора Гамильтона является обобщением классической формулы для энергии. Для множества реальных приложений теории (физика кристаллов, химия, биология) требование малости скоростей не является существенным ограничением: диапазон энергий, с которыми приходится иметь дело в земных условиях недостаточен для разгона объектов до релятивистских скоростей. Однако существует целый ряд разделов естествознания, развитие которых сделало актуальным вопрос о разработке релятивистской квантовой теории. К ним прежде всего следует отнести разделы физики, занимающиеся взаимодействием света с веществом: зародившаяся в результате попыток понять физическую природу света квантовая механика оказалась неспособной адекватно описать ультрарелятивистскую частицу — фотон. Релятивистская теория микромира необходима физике ядра и элементарных частиц, поскольку изучаемые в ее рамках процессы с участием сильных взаимодействий сопровождаются обменом большими порциями энергии, что неизбежно связано с возникновением высоких скоростей. Космологические теории эволюции Вселенной и Большого Взрыва требуют развития аппарата описания вещества в экстремальных (с нашей точки зрения) состояниях. Наконец, наличие плохо связанных друг с другом релятивистской и квантовой теорий, каждая из которых по-своему “объясняла” классическую концепцию, являющуюся предельным случаем каждой из них, неизбежно ставило вопрос об их объединении. Попытки обобщения квантовой механики и придания ей релятивистски инвариантной формы делались буквально с первых шагов ее создания, но до сих пор еще не привели к созданию законченной и полностью свободной от внутренних противоречий теории.
S-матрица. Дополнительной сложностью, присущей релятивистской теории является несохранение числа частиц, участвующих в процессе. В частности это означает, что любая рассматриваемая система должная обладать бесконечным числом степеней свободы. Поскольку сама процедура измерения координат частицы в принципе может приводить к рождению новых частиц, она становится принципиально бессмысленной. Релятивистская квантовая теория отказывается не только от описания пространственного положения микрообъектов, но и от описания процессов с их участием в виде происходящих последовательно (друг за другом) промежуточных событий. Расчеты поддаются лишь амплитуды вероятностей переходов системы из исходного состояния при , в котором все входящие в нее частицы находятся так далеко друг от друга, что взаимодействие между ними пренебрежимо мало в одно из допустимых законами сохранения конечное состояние при , в котором продукты реакции вновь являются практически свободными объектами. Набор амплитуд таких переходов образует s-матрицу, вычисление которой и является задачей релятивистской квантовой теории.
Уравнение Клейна-Гордона было первой удачной попыткой обобщения уравнения Шредингера на случай релятивистского описания электромагнитных взаимодействий микрообъектов. В основе предложенного вывода лежала идея заменить нерелятивистский оператор Гамильтона в уравнении Шредингера
на его релятивистский аналог, вид которого устанавливался на основании сравнения классических (не квантово-механических) выражений для релятивистской и нерелятивистской функций Гамильтона:
,
где учтена возможность взаимодействия зарядов с электрическим и магнитным полями, описываемыми потенциалами и A.
Основная математическая трудность, возникающая при попытке перевести релятивистскую формулу (3) на язык квантово-механических операторов состояла в том, что операция извлечения корня из оператора не определена. Предложенный выход состоял в переходе к уравнению второго порядка, возникающего при возведении в квадрат операторного аналога уравнения (3), где сам оператор Гамильтона согласно (1) заменялся на оператор дифференцирования по времени:
.
Полученное таким образом уравнение могло быть легко протестировано на хорошо изученном частном случае описания фотона (q=0, m=0). Подстановка указанных значений приводит к обыкновенному уравнению Д’Аламбера, описывающему распространение света в вакууме.
Уравнение Клейна-Гордона в настоящее время считается правильным релятивистским обобщением уравнений квантовой механики, не учитывающих наличие спина у микрообъектов. Оно адекватно оисывает http://wpgrabbestrefedu.loc/2019/01/24/utchebnaya-rabota-referat-mir-glazami-isaaka-nyyutona-prostranstvo-i-vremya/
Измерение расстояний.
неувязка ограниченности Вселенной. Измерить расстояние меж 2-мя объектами — означает сопоставить его с эталонным. До недавнешнего времени в качестве образца использовалось тело, изготовленное из твердого сплава, геометрическая форма которого слабо изменялась при изменении наружных критерий. В качестве единицы длины был избран метр, отрезок, сопоставимый с соответствующими размерами людского тела. Разумеется, что почти всегда идеал не укладывался целое число раз на длине измеряемого отрезка. Оставшаяся часть измерялась с помощью 1/10, 1/100 и т. образца. В принципе числилось, что такую функцию можно продолжать до бесконечности, в итоге чего же выходило бы четкое понятие вещественного числа появилось как итог обобщения описанной процедуры измерения длин отрезков).
На практике неоднократное деление начального образца было нереально. Для увеличения точности измерения и измерения малых отрезков потребовался идеал значительно наименьших размеров, в качестве которого по истинное время употребляются стоячие электромагнитные волны оптического диапозона.
В природе есть объекты, существенно наименьшие длин волн оптического излучения (молекулы, атомы, простые частички). При их измерениях кроме неудобства сопоставления с образцом огромных размеров возникает наиболее принципная неувязка: объекты, размеры которых меньше длины волны электромагнитного излучения, перестают его отражать и, как следует, оказываются невидимыми. Для оценки размеров таковых маленьких объектов свет подменяют потоком каких-то простых частиц (электронов, нейтронов и т.д.). Величина объектов оценивается по т.н. сечениям рассеяния, определяемым отношением числа частиц, изменивших направления собственного движения, к плотности падающего потока. Минимальным расстоянием, известным в истинное время, является соответствующий размер простой частички (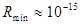
м). гласить о наименьших размерах, по-видимому, глупо.
При измерении расстояний, существенно превосходящих 1м, воспользоваться образцом длины вновь оказывается неловко. Для измерения расстояний, сравнимых с размерами Земли, используют способы триангуляции (определение большей стороны треугольника по буквально измеренной наименьшей стороне и двум углам) и радиолокации (измерение времени задержки отраженного сигнала, скорость распространения которого известна, относительно момента передачи), Для много огромных расстояний (до удаленных звезд и примыкающих галактик) обозначенные способы оказываются вновь неприменимы (отраженный радиосигнал оказывается очень слабеньким, углы треугольника различаются от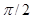 
на очень малую величину). На настолько огромных расстояниях наблюдаемыми оказываются лишь самосветящиеся объекты (звезды и галактики), расстояния до их оценивается исходя из наблюдаемой яркости.
размеры наблюдаемой части вселенной имеют размеры порядка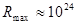 
м. вопросец о том, имеют ли смысл огромные расстояния сводится к дилеммам конечности и ограниченности Вселенной, до сего времени совсем не решенным космологией. Со времен Ньютона числилось, что окружающий нас мир однороден и не может иметь границ (в неприятном случае появлялся вопросец о их физической природе и о том, “что находится по другую сторону”). Но, предположение о бесконечности Вселенной, вместе с естественным допущением о равномерном распределении звезд по размеру и беспрепятственном распространении света в пространстве, приводил к заранее абсурдному выводу о нескончаемо ярчайшем свечении ночного неба (т.н. феномен ночного неба). Позже пришло осознание того, что понятия бесконечности и неограниченности не эквивалентны друг другу (напр. шар не имеет границ, но площадь его конечна).
Измерение интервалов времени. Возраст Вселенной.
Измерить продолжительность процесса — означает сопоставить его с эталонным. В качестве крайнего комфортно избрать какой-нибудь временами циклический процесс (суточное вращение Земли, биение людского сердца, качание маятника, движение электрона вокруг ядра атома). Длительное время в качестве эталонного процесса использовались колебания маятника. За единицу измерения времени избрали секунду (интервал, приблизительно равный периоду сокращения сердечной малая мышь«>мускулы человека).
Для измерения существенно наиболее маленьких времен появилась необходимость в новейших образцах. В их роли выступили колебания кристаллический сетки (кварцевые часы имеют соответствующий период колебаний в 1нс=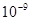 
с) и движение электронов в атоме (атомные часы с соответствующим временем 
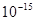с ). Еще наименьшие времена можно определять, сравнивая их со временем прохождения света через данный просвет. по-видимому, минимальным осмысленным интервалом является время прохождения света через мало вероятное расстояние (
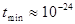с ).
С помощью маятниковых часов может быть измерение временных интервалов, существенно превосходящих 1с (людская жизнь продолжается около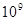 
с), да и тут способности способа не безграничны. Времена, сравнимые с годами Земли (ок. 
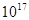с) может быть оценивать только по полураспаду атомов радиоактивных частей. Наибольшим промежутком времени, о котором имеет смысл гласить в нашем мире, по-видимому является возраст Вселенной, оцениваемый периодом в 
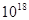с (началом существования нашего мира принято считать большенный взрыв, произошедший в очень малой области места, в итоге которого появился наблюдаемый на данный момент мир, представляющий из себя совокупа объектов, разлетающихся от исходной точки; действия, произошедшие до Огромного взрыва никак не влияют на истинное и, как следует, могут не рассматриваться).
В традиционном естествознании, занимающимся основным образом описанием макроскопических (сравнимых с размерами людского тела) объектов, предполагается, что процедура измерения главных пространственно-временных черт (расстояний и длительностей) в принципе быть может выполнена сколь угодно буквально и при всем этом может фактически не влиять на измеряемый объект и происходящие с ним процессы.
Геометрические характеристики места и времени. Геометрические характеристики места изучаются геометрией, обычно базирующейся на системе аксиом Евклида. В отличие от арифметики, для естествознания небезынтересен вопросец, соответствуют ли эти теоремы настоящим свойствам нашего места (напр. полностью мыслима ситуация, в какой сумма углов треугольника может различаться от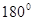 
: на рис. 2_1 изображен треугольник, все углы которого прямые). Опыт указывает, что для наблюдающего, передвигающегося без убыстрения вдалеке от мощных тел, аксиоматика Евклида производится с неплохой точностью.
Принципиальной чертой вещественных систем является их число степеней свободы (малой количество чисел, нужное для исчерпающего описания положения объекта в пространстве). Чем огромным числом степеней свободы владеет объект, тем наиболее трудоемко его описание. Возникает естественный вопросец о наименьшем числе степеней свободы, которым может владеть объект в нашем мире. Опыт указывает, что для не взаимодействующих с иными объектами тел это число равно 3 (3-мя степенями свободы владеют, к примеру, простые частички с нулевым спином). О этом свойстве нашего места молвят как о его трехмерности (время от времени молвят, что трехмерность значит возможность задания 3-х взаимно перпендикулярных направлений в пространстве). Число степеней свободы большинства настоящих объектов быть может значительно огромным (спортивный велик с отлично затянутыми болтами и гайками владеет как минимум 18 степенями свободы), но при решении почти всех практических задач “внутренние степени свободы” оказываются несущественными (на финише велогонки положение педалей велика фаворита никем не регится). Число рассматриваемых степеней свободы можно значительно уменьшить прямо до 3-х (при движении в пространстве), 2-ух (при движении по поверхности) либо одной (при движении вдоль данной кривой). Реальное тело при всем этом по существу заменяется моделью вещественной точки (тело, размеры и форма которого в рассматриваемой ситуации несущественны).
Для задания временных черт действий может пригодиться несколько вещественных чисел (жизнь человека можно охарактеризовывать, к примеру, моментами его рождения, женитьбы и погибели). Но есть явления, для исчерпающего временного описания которых довольно 1-го числа (напр. распад простой частички, который не имеет продолжительности, так как не быть может разбит на какие-то промежные процессы). Существование таковых “простых” действий дозволяет утверждать, что время одномерно.
Аналогично тому, как в пространственном описании вводилась модельное времени можно ввести понятие моментального действия, т.е. процесса, продолжительностью которого в рассматриваемой ситуации можно пренебречь (напр. удар мяча о стенку нередко можно считать моментальным, хотя детализированное рассмотрение указывает, что это очень непростой и многоэтапный процесс).
Относительность параметров места и времени. Во времена Ньютона числилось, что характеристики места и времени абсолютны, т.е. не зависят от наличия вещественных тел, протекающих действий и наблюдателей. Современная физика показала ограниченность таковых представлений: геометрические характеристики места и времени тесновато соединены с наличием и расположением мощных тел, зависят от нрава протекающих действий и даже от состояния наблюдающего. В связи с сиим на данный момент принято гласить, что характеристики места и времени относительны.
В традиционном естествознании рассматриваются макроскопические объекты и явления, происходящие в имеющихся независимо от их и друг от друга пространстве и времени, носящих абсолютный нрав.
]]>