Учебная работа. Реферат: Золотое сечение в природе и искусстве

Учебная работа. Реферат: Золотое сечение в природе и искусстве

Золотое сечение в природе и искусстве

Создатель: Седлинский Игорь Николаевич

Гимназия № 1 г. Апатиты, Мурманская обл.

4-ая региональная научная и инженерная выставка «Будущее Севера»

Мурманск

2002 год

Геометрия обладает 2-мя сокровищами: одно из их – аксиома Пифагора, другое- деление отрезка в среднем и последнем отношении.

И. Кеплер

человек различает окружающие его предметы по форме. Энтузиазм к форме какого-нибудь предмета быть может продиктован актуальной необходимостью, а быть может вызван красотой формы. Форма, в базе построения которой лежат сочетание симметрии и золотого сечения, содействует лучшему зрительному восприятию и возникновению чувства красы и гармонии. Целое постоянно состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и многофункционального совершенства целого и его частей в искусстве, науке, технике и природе.

Самым известным из всех иррациональных чисел, другими словами чисел, десятичные разложения которых нескончаемы и непериодичны, следует считать число p – отношение длины окружности к ее поперечнику. Иррациональное число j («фи») понятно не настолько обширно, но оно выражает базовое отношение, имеющее практически таковой же всепригодный нрав, как и число p. Сходство меж числами p и j сиим не исчерпывается: подобно p, j владеет свойством возникать в самых нежданных местах .

Что такое золотая пропорция.

Пусть длина некого отрезка равна А (рис.1) , длина его большей части равна Х, тогда (А – Х) – длина наименьшей части отрезка. Пусть отношение всего отрезка к большей его части равно отношению большей части к наименьшей. Составим отношение согласно допущению: 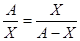. (1)

Такое деление отрезка и именуется со времен старых греков делением отрезка в последнем и среднем отношении.

От пропорции (1) перейдем к равенству A(A-X)=X2 . Получаем квадратное уравнение 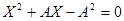. Длина отрезка X выражается положительным числом, потому из 2-ух корней избираем положительный: .

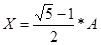Число 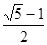обозначается буковкой j либо буковкой t («тау») в суровой арифметике. Не наименее принципиальное

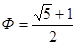=1/j

Обратим внимание на изумительную инвариантность золотой пропорции:

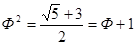
Такие значимые преобразования, как возведение в степень, не смогли убить суть данной неповторимой пропорции, ее «душу». Последующие соотношения снова показывают инвариантность золотой пропорции:

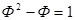
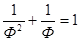
-2-

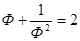
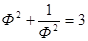и т.д.

Подобно числу p ,Ф можно представить в виде суммы нескончаемого ряда почти всеми методами. Предельная простота последующих 2-ух примеров снова подчеркивает базовый нрав Ф :

Ф =lim 1+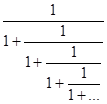

Ф = lim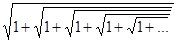

С золотой пропорцией тесновато связан ряд чисел Фибоначчи 1,1,2,3,5,8,13,21,34,55,89 и т.д. В этом ряду каждое следующее число является суммой 2-ух прошлых чисел. Спустя четыре столетия опосля открытия Фибоначчи ряда чисел И.Кеплер установил, что отношение стоящих чисел в пределе стремится к золотой пропорции Ф. Это свойство присуще не только лишь числам Фибоначчи. Начав с всех 2-ух чисел и построив аддитивный ряд, в каком любой член равен сумме 2-ух прошлых (к примеру, ряд 7, 2, 9, 11, 20, …), мы нашли, что отношение 2-ух поочередных членов такового ряда также стремится к числу j: чем далее мы будем продвигаться от начала ряда, тем лучше будет приближение.

В предстоящем увидим, что числа Фибоначчи нередко возникают в самых нежданных местах, при всем этом неотступно сопровождая золотую пропорцию.

Золотые фигуры.

В геометрии есть разные методы построения золотой пропорции, при этом типично, что для построения довольно взять самые обыкновенные геометрические фигуры – квадрат либо прямоугольный треугольник с соотношением катетов 1:2. Если с середины стороны квадрата провести окружность радиусом, равным диагонали полуквадрата, то на ее пересечении с продолженной стороной квадрата получим отрезок, который меньше стороны квадрата в согласовании с золотой пропорцией. Еще проще построение золотой пропорции в прямоугольном треугольнике 1:2: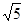 . Довольно провести две дуги окружности, пересекающиеся в одной точке на гипотенузе (рис.2), и большенный катет будет разбит в согласовании с золотой пропорцией.

Золотое сечение можно узреть и в пентаграмме — так называли греки звездчатый многоугольник (рис.3). Он служит эмблемой Пифагорейского союза – религиозной секты и научной школы по главе с Пифагором, которая проповедовала братскую любовь к друг другу, отречение от наружного мира, общность имущества и т.д. На схожих устоях основывались весьма почти все секты . Но Пифагорийский альянс отличало от остальных то, что пифагорейцы считали вероятным достигнуть очищения духа с помощью арифметики. По их теории, в базу мирового порядка положены числа. мир, считали они, состоит из противоположностей, а гармония приводит противоположности к единству. Гармония же заключается в числовых отношениях. Пифагорейцы причисляли числам разные характеристики. Так, четные числа они называли женскими, нечетные (не считая 1) – мужскими. Число 5 – как сумма первого дамского числа (2) и первого мужского (3) – числилось эмблемой любви. Отсюда такое внимание к пентаграмме, имеющей 5 углов.

Благоговейное отношение к пентаграмме было типично и для средневековых мистиков, которые почти все заимствовали у пифагорейцев. В средние века числилось, что пентаграмма служит охранным знаком от сатаны. Вспомним, к примеру, как обрисовывает Гете проникновение беса Мефистофеля в келью доктора Фауста, на которой была начертана пентаграмма. Мефистофель поначалу послал темного пуделя отгрызть краешек двери с частью пентаграммы. Лишь опосля этого он сумел стать перед Фаустом.

Любопытно, что стороны пентаграммы, пресекаясь, образуют верный пятиугольник, в каком пресечение диагоналей дает нам новейшую пентаграмму, а в пересечении ее сторон мы опять лицезреем верный пятиугольник, открывающий возможность построения новейшей пентаграммы. И так дальше до бесконечности.

Пентаграмма представляет собой вместилище золотых пропорций. На рис.3 посреди отрезков HJ, EH, EJ, EB отношение всякого следующего к предшествующему равно золотой пропорции. Пентаграмма также содержит золотые треугольники –остроугольные с углами 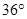,,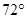 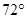и тупоугольные с углам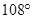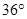и , и 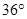.Из рис. 4 видно, что остроугольный треугольник АВС разбивается на три треугольника золотой пропорции. В их стороны равны:AD=1, DB=Ф,BC=AB=Ф+1=Ф2,AC=AE=Ф.

Увлекателен очередной превосходный треугольник, в каком проявляется золотая пропорция. В этом треугольнике углы равны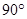, 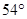и 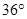, а их отношение составляет 5:3:2. В нем отношение огромного катета к гипотенузе равно половине золотой пропорции Ф/2. Это отношение отвечает равенству Ф/2 = cos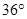. Отсюда вытекает формула , связывающая золотую пропорцию с числом p:

Ф= .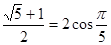

Эта обычная и по-своему прекрасная формула связывает число «пи» с золотой пропорцией. Не свидетельствует ли это о фундаментальности золотой пропорции, о ее родстве с таковым всепригодным числом, как «пи»? Типично, что в рассмотренном треугольнике отношение углов отвечает отношению маленьких целых чисел 5, 3 и 2, а дела сторон несоизмеримы.

Огромное количество «золотых» фигур дополняет золотой прямоугольник, отношение сторон которого равно числу Ф.

Золотой прямоугольник владеет почти всеми необыкновенными качествами. Отрезав от него квадрат, сторона которого равна наименьшей стороне прямоугольника, мы опять получим золотой прямоугольник наименьших размеров. Продолжая отрезать квадраты, мы будем получать все наименьшие и наименьшие золотые прямоугольники (рис.5)

Тем будет построен пример совершенного квадрируемого прямоугольника нескончаемого порядка. Точки, делящие стороны прямоугольников в среднем и последнем отношении, лежат на логарифмической спирали, закручивающейся вовнутрь. Полюс спирали лежит на пересечении пунктирных диагоналей (рис.6). Очевидно, «крутящиеся квадраты», как их принято именовать, могут не только лишь закручивать, да и раскручивать спираль. Для этого только требуется строить не уменьшающиеся, а все увеличивающиеся квадраты. Логарифмическая спираль – единственный тип спирали, не меняющей собственной формы при увеличении размеров. Если в логарифмической спирали из центра О провести прямую, то образующиеся отрезки ОА, ОВ, ОС, ОD и т. д., приобретенные при пересечении прямой с витками спирали, образуют геометрическую прогрессию, другими словами ОА/ОВ=ОВ/ОС=ОС/OD=…= m, где m – неизменное число.

Отрезки радиуса, заключенного меж поочередными витками спирали, также образуют прогрессию с отношением АВ/ВС=ВС/СD=…=n. Личным случаем спирали является таковая, которая отвечает значению n, равному Ф, т. е. золотой пропорции. Таковая спираль именуется «кривой гармонического возрастания».

Всесущий филлотаксис.

Соответствующей чертой строения растений и их развития является спиральность. Еще Гете, который был не только лишь величавым поэтом, да и естествоиспытателем, считал спиральность одним из соответствующих признаков всех организмов, проявлением самой заветной сути жизни. Спирально закручиваются усики растений, по спирали происходит рост ткани в древесных стволах, по спирали размещены семена в подсолнечнике, спиральные движения (нутации) наблюдаются при росте корней и побегов. Разумеется, в этом проявляется наследственностьорганизации растений, а ее корешки следует находить на клеточном и молекулярном уровнях.

Исследования проявили, что движение протоплазмы в клеточке нередко спиральное. Рост клеток также быть может спиральным, как показал ученый Кастл. В водянистой среде клеточки встречаются спиральные нити волокон – цитонем. И, в конце концов, носители инфы – молекулы ДНК – также скручены в спираль. Необходимо подчеркнуть, что термин «спираль» не отражает буквально строение молекул ДНК ; наиболее верно гласить о винтообразном расположении полипептидных цепей в данной молекуле. В почти всех остальных вариантах, рассмотренных в ботанике, речь также идет, по существу, не о спирали, а о винтообразном расположении частей структуры; к огорчению, определения нередко соединяют.

Нет колебаний, что наследная спиральность является одним из главных параметров организмов, она отражает один из существенных признаков живого. На 1-ый взор кажется, что в кристаллах неорганических веществ спиральность либо винтообразная структура отсутствуют. Но наиболее глубочайшие исследования проявили, что винтообразное размещение атомов наблюдается и в неких кристаллах и выражается в образовании так именуемых винтообразных дислокаций. Такие кристаллы состоят из единственной винтовой изогнутой атомной плоскости. При любом обороте вокруг оси эта плоскость поднимается на один шаг винта, равный межатомному расстоянию. Следует добавить, что кристаллы с таковой винтообразной структурой владеют сверхпрочностью. От винтообразной структуры молекул ДНК до закручивания усиков растений – таковы формы проявления спиральности на разных уровнях организации растений. ясно проявляется эта изюминка организации растений в закономерностях листорасположения.

Существует несколько методов листорасположения. В первом листья побега размещаются строго один под иным, образуя вертикальные ряды – ортостихи. Условная спираль, соединяющая места расположения листьев на побеге, именуется генетической, либо главный спиралью, поточнее, винтообразной линией и делится на ряд листовых циклов. Генетическим этот винт именуется поэтому, что размещение листьев в нем отвечает порядку возникновения в нем листьев. 1-го листового цикла, а знаменатель- числу листьев в данном цикле, совпадающему с числом ортостих на стебле. Эта дробь дозволяет высчитать и угол расхождения листьев.

Оказалось, что каждое растение характеризуется своим листорасположением. Так, у липы, вяза, бука, злаков листорасположение описывается формулой 1/2, у дуба и вишни – 2/5, у малины, груши, тополя, барбариса – 3/8, у миндаля, облепихи – 5/13 и т.д. Несложно созидать, что в формулах листорасположения встречаются числа Фибоначчи, расположенные через одно.

Поглядим на сосновую шишку. Чешуйки на ее поверхности размещены строго закономерно — по двум спиралям, которые пересекаются примерно под прямым углом. Число таковых спиралей у сосновых шишек равно 8 и 13 либо 13 и 21 . Такие же спирали видны в поперечных разрезах почек; тут числа спиралей относятся

как числа 3/5, 5/8, 8/13. В плетенках подсолнечника семечки также размещены по

-5-

двум спиралям, их число составляет обычно 34 и 55, 55 и 89. тут вновь мы лицезреем закономерное сочетание чисел Фибоначчи, расположенных : 2/3, 3/5, 5/8, 13/21 и т.д. Их отношение в пределе стремится к числу j = 0,61803…

Рассмотренную закономерность расположения листьев, чешуек, семян именуют филлотаксисом.

При изменении формулы листорасположения меняется и угол расхождения листьев. Формула 1/2 охарактеризовывает двурядное размещение листьев под углом 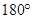друг от друга. При формуле 1/3 угол меж листьями будет 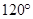, а при формуле 2/5 — 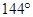и т.д. В предельном случае, когда отношение чисел в формуле будет отвечать золотой пропорции — 0,38196… угол расхождения листьев станет равным 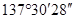, который был назван «безупречным» углом, либо углом золотой пропорции ( 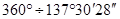=Ф2). Установлено, что при расположении листьев под безупречным углом ни один лист не будет размещаться буквально над иным, чем создаются наилучшие условия для фотосинтеза.

Загадки египетских пирамид.

Все в мире боится времени. А время боится пирамид.

Арабская пословица

О египетских пирамидах с восхищением писал греческий историк Геродот. Первым европейцем, спустившимся в глубь пирамиды, был римский ученый Плиний Старший. Согласно почти всем описаниям, эти огромные монолиты имели совершенно другой вид, чем в наше время. Они светились на солнце белоснежной глазурью отполированных известняковых плит на фоне многоколонных прилегающих храмов. с королевскими пирамидами стояли малые пирамиды жен и членов семьи фараонов.

Посреди превосходных пирамид Египта особенное пространство занимает величавая пирамида фараона Хеопса. Она самая большая и более отлично изученная. Чего же лишь не находили в ее пропорциях! Число «пи» и золотую пропорцию, число дней в году, расстояние до Солнца, поперечник Земли и т.п. Но при расчете этих величин выходили некорректности, появлялись недоразумения, в итоге чего же подвергались сомнению даже простые пропорции в размерах пирамиды и все сообщения о укрытых в геометрии пирамиды математических сведениях объявлялись выдумкой.

Верная четырехгранная пирамида является одной из отлично изученных геометрических фигур, символизирующих простоту и гармонию формы, олицетворяющую устойчивость, надежность, устремление ввысь.

Разумеется, размеры пирамиды: площадь ее основания и высота — не были выбраны случаем, а должны нести какие-то геометрические, математические идеи, информацию о уровне познаний египетских жрецов. При этом следует напомнить, что эти познания составляли тайну и были доступны только ограниченному числу лиц, потому и в геометрии пирамиды они должны быть воплощены не в очевидной, а в сокрытой форме.

Методической ошибкой почти всех исследователей будет то, что они употребляли размеры пирамид, выраженные в метрической системе мер. Но ведь египтяне воспользовались иной системой мер! Из данной системы и следует исходить при анализе размерных отношений в пирамидах.

До этого чем приступить к анализу формы и размеров пирамиды Хеопса, следует учитывать уровень познаний тех времен, психологию создателей пирамиды. У египтян было три единицы длины: локоть (466 мм), равнявшийся 7 ладоням (66,5 мм), которая, в свою очередь, равнялась четырем пальцам (16,6 мм).

Тяжело допустить, что строители пирамиды воспользовались начальными размерами, выраженными в толиках локтя; наиболее разумеется, что главные начальные размеры были определены в целых единицах длины – локтях.

Разглядим размеры пирамиды Хеопса (рис.7). Длина стороны основания пирамиды (L) принята равной 233,16 м. Эта величина отвечает практически буквально 500 локтям. Разумеется, размер основания пирамиды при ее строительстве и был определен в 500 локтей.

Высота пирамиды (H) оценивается исследователями различно от 146,6 до 148,2 м. И зависимо от принятой высоты пирамиды меняются и все дела ее геометрических частей. Потому на данной величине следует тормознуть особо. Одним из чудес величавой пирамиды является весьма четкая подгонка ее каменных блоков и плит; меж ними практически нигде не просунешь лезвия бритвы (0,1 мм). Но никакого чуда тут не оказалось. В процессе строительства каменные блоки не могли быть сделаны настолько буквально: для этого у старых египтян просто не было средств – ни обрабатывающих, ни измерительных. Но за долгое время под действием колоссального давления (достигающего 500 тонн на 1 м2 нижней поверхности) произошла «усадка» конструкции, пластическая деформация строй блоков, вследствие чего же они и оказались так тесновато подогнанными. В итоге усадки высота пирамиды стала меньше, чем она была в период окончания строительства. Какой она была сначало? Ее можно воссоздать, если отыскать основную «геометрическую идею», положенную в базу сооружения.

Угол наклона граней пирамиды еще в 1837 году обусловил британский полковник Г.Вайз: он равен . Обозначенному значению угла отвечает тангенс, равный 1,272. Эта величина, отвечающая отношению высот пирамиды к половине ее основания, весьма близка к корню квадратному из золотой пропорции 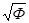= 1,27202 и является иррациональной величиной. Потому, быстрее всего, в базу треугольника OMN пирамиды Хеопса и было заложено отношение OM/MN, равное .

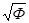Итак, примем отношение катетов, т.е. высоты пирамиды H к половине ее основания, равным 1,272. При всем этом высота пирамиды Хеопса будет равна буквально 318 локтей, либо 148,28 м. Такую высоту, разумеется, имела пирамида Хеопса при окончании ее сооружения ( либо обязана была иметь по проекту).

Таковым образом, главные элементы конструкции пирамиды имели последующие размеры: сторона основания – 500 локтей, высота – 318 локтей. Отсюда следует, что апофема боковой грани ON равна 404,5 локтя.

А сейчас поглядим, какие достойные внимания соотношения следуют из этих геометрических размеров. дела сторон в треугольнике OMN пирамиды равно: OM/MN=ON/OM=1,272=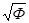; ON/MN=Ф.

Разглядим сейчас поверхность пирамиды. Она состоит из 4 треугольников и квадрата основания. Основание треугольника BOC равно 500 локтям, высота его равна 404,5 локтя. По аксиоме Пифагора можно высчитать длину боковых ребер OB и OC . Они равны 475,5 локтя.

Площадь основания пирамиды равна 250000 кв. локтей, площадь боковой грани 101125 кв. локтей, а площадь 4 граней пирамиды равна 404500 кв. локтей. Отношение поверхности граней к площади основания также равно золотой пропорции.

Еще Геродот, основываясь на рассказах египетских жрецов, писал, что площадь квадрата, построенного на высоте пирамиды, равна площади каждой из его боковых граней. По нашим расчетам, квадрат высоты равен 3182 = 101127 кв. локтей, что практически буквально отвечает площади боковой грани (101125 кв. локтей).

Почти все исследователи указывают, что отношение двойной стороны основания 2L к высоте пирамиды H отвечает числу «пи». Но в связи с тем, что высота пирамиды принималась равной современной и не постоянно конкретной, число «пи» выходило различным: 3,16-3,18. На почве этого появлялись сомнения, предпринимались разные подгонки, стали гласить даже о некоем «египетском p», равном 3,16. Если принять высоту пирамиды равной 318 локтям, то отношение 2L/H=1000/318 будет равно 3,144. Эта величина весьма близка к современному значению числа «пи» (3,14159…).

Любопытно сопоставить два главных дела, установленных нами при исследовании геометрических пропорций пирамиды: 2H/L=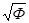 и 2L/H=p. Отсюда получаем ординарную и прекрасную формулу, связывающую число «пи» и золотую пропорцию: 4/p=.

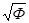Превосходные создатели пирамиды Хеопса стремились поразить дальних потомков глубиной собственных познаний, и они достигнули этого. Следует только удивляться высочайшему познанию и искусству старых математиков и архитекторов Египта, которые смогли воплотить в пирамиде две иррациональные (т.е. неизмеримые) величины – p и Ф со настолько поразительной точностью, оперируя начальными отношениями целых чисел – стороной основания и высотой пирамиды, выраженных в локтях.

Золотая пропорция в искусстве Старой Греции.

Прекрасные монументы архитектуры оставили нам зодчие Старой Греции. И посреди их 1-ое пространство по праву принадлежит Парфенону.

Всю вторую половину V в. до н.э. на Акрополе шло стройку храмов, пропилей (преддверий), алтаря и скульптуры Афины Воительницы. В 447 году начались работы над храмом Афины – Парфеноном и длилось до 434 года до н.э. Для сотворения гармонической композиции на холмике его строители даже прирастили бугор в южной части, соорудив для этого сильную насыпь.

Как показывает исследователь Г. И. Соколов, протяженность холмика перед Парфеноном, длины храма Афины и участка Акрополя за Парфеноном относятся как отрезки золотой пропорции. При взоре на Парфенон от места расположения пропилей дела массива горы и храма также соответствуют золотой пропорции. Таковым образом, золотая пропорция была применена уже при разработке композиции храмов на священном холмике.

размеры Парфенона отлично исследованы, но приводимые замеры не постоянно однозначны. Следует учитывать, о чем сказано ниже, что геометрия архитектуры храма весьма сложная – в ней практически отсутствуют прямые полосы, потому определение размеров затруднено. Понятно, что фасад Парфенона вписан в прямоугольник со сторонами 1 : 2 , а план образует прямоугольник со сторонами 1 и 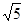. Понятно, что диагональ прямоугольника 1:2 имеет размер 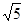, как следует, прямоугольник фасада и является начальным в построении геометрии Парфенона.

Ширина Парфенона оценена в 100 греческих футов (3089 см), а размер высоты несколько варьирует у разных создателей. Так, по данным Н. Бруно, высота Парфенона 61,8 , высота 3-х ступеней основания и колонны – 38,2 , высота перекрытия и фронтона – 23,6 футов. Обозначенные размеры образуют ряд золотой пропорции: 100 : 61,8 = 61,8 : 38,2 = 38,2 :23,6 = Ф.

Почти все исследователи, стремившиеся раскрыть секрет гармонии Парфенона, находили и находили в соотношениях его частей золотую пропорцию. В работе В.Смоляка, посвященной исследованию пропорций Парфенона, установлен закономерный ряд золотых пропорций. Приняв за единицу ширину торцового фасада храма, Смоляк получил прогрессию, состоящую из 8 членов ряда: 1: j: j2: j3: j4: j5: j6. Обозначенным членам ряда отвечают главные пропорции фасада Парфенона (рис.8).

В неких сооружениях старого мира золотая пропорция выражена не в пропорциях формы спостроек, а в деталях внутренней композиции, даже в числе мест для зрителей. Достойные внимания данные приводит Э.Сороко. Построенный Поликлетом-младшим театр был рассчитан на 15 тыщ зрителей. Места для зрителей (театроп) имели 2 яруса : первый- 34 ряда мест, а 2-ой – 21 ряд (числа Фибоначчи). Раствор угла , обхватывающего место меж театропом и скемой (пристройка для переодевания актеров и хранения реквизита), разделяет окружность основания амфитеатра в отношении 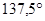: 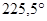, что равно 1: 1,618…. Это соотношение углов реализовано фактически во всех древних театрах. Театр Диониса в Афинах трехъярусный. 1-ый ярус имеет 13 секторов, 2-ой – 21 сектор.

Древнейшие архитекторы знали и употребляли золотую пропорцию как аспект гармонии, канон красы, корешки которой лежат в пропорциях людского тела. “Тело человека – наилучшая краса на земле”, — утверждал Н.Чернышевский. Образцами красы людского тела, эталонами гармонического телосложения давно и по праву числятся величавые творения греческих архитекторов: Фидия, Поликлета, Мирона, Праксителя. В разработке собственных творений греческие мастера употребляли принцип золотой пропорции. Центр золотой пропорции строения людского тела размещался буквально на месте пупка. И не случаем величину золотой пропорции принято обозначать буковкой Ф; это изготовлено в честь Фидия – творца бессмертных скульптурных произведений.

Одним из высших достижений традиционного греческого искусства может служить скульптура “Дорифор”, изваянная Поликлетом. Фигура юноши выражает единство красивого и доблестного, лежащих в базе греческих принципов искусства. Широкие плечи практически равны высоте тела, высота головы восемь раз укладывается в высоте тела , а золотой пропорции отвечает положение пупка на теле атлета.

Но проанализируем остальные пропорции известной скульптуры. Расстояние от подошвы копьеносца до его колена равна j3, высота шейки совместно с головой — j4, длина шейки до уха — j5, а расстояние от уха до маковки — j6 . Таковым образом, в данной статуе мы лицезреем геометрическую прогрессию со знаменателем j: 1, j, j2, j3, j4, j5, j6. (рис.9).

Таковым образом, золотое сечение – один из основополагающих принципов в искусстве древней Греции.

Ритмы сердца и мозга .

Умеренно бьется сердечко человека – около 60 ударов за минуту в состоянии покоя. обеспечивающий ток крови по кровеносным сосудам»>сердечко

как поршень сжимает , а потом выталкивает образованная жидкой соединительной тканью. Состоит из плазмы и форменных элементов: клеток лейкоцитов и постклеточных структур: эритроцитов и тромбоцитов»>тканью. Состоит из плазмы и форменных элементов: клеток лейкоцитов и постклеточных структур: эритроцитов и тромбоцитов) в несущие образованная жидкой соединительной тканью. Состоит из плазмы и форменных элементов: клеток лейкоцитов и постклеточных структур: эритроцитов и тромбоцитов»>кровь от сердца к органам . Кровеное давление меняется в процессе работы сердца. Большей величины оно добивается в левом желудочке в момент его сжатия (систолы) . В артериях во время систолы желудочков давление крови добивается наибольшей величины, равной 115-125 мм рт.ст. у здорового юного человека. В момент расслабления сердечной мускулы (диастолы) давление понижается до 70-80 мм рт.ст. Отношение наибольшего (систолического ) к минимальному (диастолическому) давлению равно в среднем 1,6 ,т.е. близко к золотой пропорции.

погибели. Его работа обязана быть хорошей, обусловленной законами самоорганизации био систем. Отличия от рационального режима вызывают разные работоспособности»>естественно представить, что и в работе сердца может быть проявление этого аспекта. Необходимы были глубочайшие исследования, и они были проведены русским ученым В.Д.Цветковым.

При работе сердца возникает электронный ток, который можно поймать особым устройством и получить кривую – электрокардиограмму (ЭКГ ) с соответствующими зубцами, отражающими разные циклы работы сердца. На ЭКГ человека выделяются два участка различной продолжительности, надлежащие систолической и диастолической деятель сердца. В.Растений установил, что у человека и у остальных млекопитающих имеется лучшая («золотая») частота сердцебиения, при которой продолжительности систолы, диастолы и полного сердечного цикла соотносятся меж собой в пропорции 0,382 : 0,618 : 1 , т.е. в полном согласовании с золотой пропорцией. Так, к примеру, для человека эта частота равна 63 ударам за минуту, для собак – 94 , что отвечает настоящей частоте сердцебиения в состоянии покоя.

Дальше В.Растений нашел, что систолическое давление крови в аорте равно 0,382 , а диастолическое – 0,618 от среднего давления крови в аорте. Толика размера левого желудочка при ударном выбросе крови по отношению к конечнодиастолическому размеру у 10 видов млекопитающих в состоянии покоя составляет 0,37-0,4 , что в среднем также отвечает золотой пропорции. Таковым образом, работа сердца в отношении временных циклов, конфигурации кровяного давления и размеров желудочков оптимизировано по одному и тому же принципу – по правилу золотой пропорции.

деятель разных органов людского тела, воплощение связи человека с окружающей средой. В составе мозга различают сероватое и белоснежное вещества. Сероватое вещество представляет собой скопление орган животного, служащий для передачи в мозг важной для организма информаци) волокон, отростков этих клеток. Нервная клеточка с отростком именуется нейроном. Нейроны мозга образуют различные сети, взаимодействующие при помощи электронных сигналов.

Конфигурации нейронных сетей представляют собой колебательные электронные цепи. Разным состояниям мозга соответствуют электронные колебания с различными частотами.

Бессчетные исследования проявили, что в мозгу взрослого человека при разных его состояниях преобладают электронные колебания определенных частот. Изменение активации мозга происходит не безпрерывно, а лишь дискретно, скачками от 1-го уровня к другому. Любому состоянию мозга соответствуют свои специальные волны электронных колебаний.

Состоянию размеренного бодрствования отвечает более устойчивый a- ритм с частотами колебаний в большей степени от 8 до 13 герц. Это главный ритм электронных колебаний мозга , он возникает в детском возрасте и равномерно с годами возрастает с 2-3 до 8-13 гц в возрасте 8-16 лет. Более неспешные колебания с частотой 0,5 –4 гц у D- ритма, типично для состояния глубочайшего сна. Для D- ритма верхняя граничная частота довольно размеренна и равна 3-4 гц, а пределы нижней граничной частоты меняются от 0,2 до 1,5 гц.

При возникновении проблемы либо угрозы в мозгу доминирует q — ритм с частотами от 4-7 до 6-8 (по данным разных создателей). Русские ученые-братья Я.и А. Соколовы считают, что более устойчивы для q- ритма граничные частоты колебаний 4 — 7 гц. Интеллектуальной работе отвечает b- ритм с граничными частотами 14-35гц. (по иным данным, спектр частот этого ритма наиболее широкий – от 14 до 100гц). Чувственному возбуждению мозга соответствует g- ритм с граничными частотами 35-55 гц. Несложно увидеть, что граничные частоты ритмов практически буквально отвечают числам Фибоначчи. Отличия граничных частот от чисел Фибоначчи находятся в границах точности опыта. Соколовы считают, что есть еще не обнаруженные опытами r- ритм и s- ритм. Расчеты проявили, что у s- ритма пограничные частоты 118 и 225 гц, а у r- ритма — 55 и 118 гц. И тут явна близость чисел Фибоначчи.

Исследования в данной области лишь начинаются, впереди — открытие самых заветных загадок организации и работы мозга человека, закономерности его эволюции.

Алгебра музыки.

В композиции почти всех музыкальных произведений отмечается наличие некого «кульминационного взлета», высшей точки, при этом такое построение типично не только лишь для произведения в целом, да и для его отдельных частей. Таковая высшая точка очень изредка размещена в центре произведения либо его композиционной части, обычно она смещена, асимметрична. Изучая восьмитактные мелодии Бетховена, Шопена, Скрябина, русский музыковед Л.Мазель установил, что в почти всех из их верхушка, либо высшая точка, приходится на сильную долю шестого такта либо на последнюю маленькую долю 5-ого такта, т.е. находится в точке золотого сечения. По воззрению Л.Мазеля, число схожих восьмитактов, где подъем мелодии занимает 5 тактов, а следующий спуск – три, необыкновенно велико. Их можно без усилий отыскать практически у всякого создателя, сочинявшего музыку в гармоническом стиле.

Разумеется, такое размещение кульминационных моментов музыкальной мелодии является принципиальным элементом ее гармонической композиции, придающим художественную выразительность и эстетическую чувственность мелодии.

Типично, что в неких вариантах создатели музыкальных произведений сдвигали их верхушку от точки золотого сечения, что присваивало мелодиям неуравновешенный нрав. По воззрению Л.Мазеля, это входило в намерения создателей, к примеру, при сочинении скерцо, рондообразных концов.

Более пространное исследование проявлений золотого сечения в музыке было предпринято Л.Сабанеевым. Им было исследовано две тыщи произведений разных композиторов. По его воззрению, временное протяжение музыкального произведения делится «некими вехами», которые выделяются при восприятии музыки и упрощают созерцание формы целого. Все эти музыкальные вехи делят целое на части, обычно, по закону золотого сечения.

По наблюдениям Л.Сабанеева, в музыкальных произведениях разных композиторов обычно констатируется не одно золотое сечение, а целая серия схожих сечений. Каждое такое сечение отражает свое музыкальное событие, высококачественный скачок в развитии музыкальной темы. В изученных им 1770 сочинениях 42 композиторов наблюдалось 3275 золотых сечений. количество произведений, в каких наблюдалось хотя бы одно золотое сечение, составило 1338. Наибольшее количество музыкальных произведений, в каких имеется золотое сечение, у Аренского (95%), Бетховена (97%), Гайдна (97%), Моцарта (91%), Скрябина (90%), Шопена (92%), Шуберта (91%).

Более детально были исследованы все 27 этюдов Шопена. В их найдено 154 золотых сечения; всего в 3-х этюдах золотое сечение отсутствовало. В неких вариантах строение музыкального произведения соединяло внутри себя симметричность и золотое сечение сразу; в этих вариантах оно делилось на несколько симметричных частей, в каждой из которых проявляется золотое сечение. У Бетховена также сочинения делятся на две симметричные части, а снутри каждой из их наблюдаются проявления золотой пропорции.

Типично, что более нередко золотое сечение находится в произведениях высокохудожественных, принадлежащих превосходным создателям. Быть может, частота проявлений золотой пропорции является одним из беспристрастных критериев оценки гениальности музыкальных произведений и их создателей?

Итак, можно признать, что золотая пропорция является аспектом гармонии композиции музыкального произведения.

Музыка стихов.

Почти все в структуре произведений поэзии роднит этот вид искусства с музыкой. Любой стих владеет собственной музыкальной формой – собственной ритмикой и мелодией. Можно ждать, что в строении стихотворений проявятся некие черты музыкальных композиций, закономерности музыкальной гармонии, а как следует, и золотая пропорция, и числа Фибоначчи.

Исследования поэтических произведений с этих позиций лишь начинаются. И начинать необходимо с поэзии А.С.Пушкина. Ведь его произведения — эталон более выдающихся творений российской культуры, эталон высокого уровня гармонии. С поэзии А.С.Пушкина мы и начнем поиски золотой пропорции – измеряла гармонии и красы.

Для анализа метрики стихотворений А.С.Пушкина рассмотрены его произведения периода 1829-1836 г.г., периода сотворения более совершенных стихов. Сюда вошло 109 стихов. Число строк в стихотворениях этого периода изменялось от 4 до 116. Но огромные стихотворные формы встречаются изредка; число стихотворений с количеством строк наиболее 60 составило всего 9 штук. Средний размер этих стихотворений составил 88 строк.

Чудилось бы, величина стихотворения, определяемая числом строк, может изменяться произвольно и безпрерывно от самой малой в четыре строчки до самых огромных. Но оказалось, что это не так. размеры стихов распределены совершенно не умеренно; выделяются желательные и изредка встречающиеся размеры. На графике распределения стихотворений А.С.Пушкина по числу строк в их ясно выделяется несколько максимумов — более встречающихся размеров (рис.10). Они очевидно тяготеют к числам 5, 8, 13, 21, 34. Проявляется полностью закономерная тенденция в творческой манере поэта – он очевидно предпочитает стихотворения, размер которых близок к числам ряда Фибоначчи.

Лишь ли стихотворения А.С. Пушкина тяготеют в собственных размерах к числам Фибоначчи?

естественно, нет. И у остальных поэтов проявляется тяготение размера стихов к 8,13,21 строкам, но ни у 1-го из российских поэтов эта тенденция не выражена так ясно, как у А.С.Пушкина. Стихотворения В.Брюсова различаются совершенством собственных форм. И логично, что в их размерности также появляются числа Фибоначчи. Было проанализировано 360 стихотворений поэта из его двухтомника; эти стихи обхватывали период от 1882 до 1912 года. Лишь в 3-х стихотворениях число строк составило 70, 85, 90 (что в среднем близко к числу Фибоначчи 89). Другие стихотворения содержали существенно меньше строк – от 8 до 36 и очень изредка несколько больше.

Посреди рассмотренных стихотворений В.Брюсова очевидно преобладают те, в каких число строчек равно либо близко к числам Фибоначчи. Они распределены последующим образом:

стихотворения с числом строк 8 25 шт. 7%

— * — 131 77 шт. 21,5% — * — 211 70 шт. 19,6% — * — 342 36 шт. 10,0%

Общее число этих стихотворений составило 208 шт. либо 58%. К остальным относятся стихотворения с числом строчек 10, 14, 16, 18, 24, 26, 28, 31 , 32 и т.д. Поэт очевидно предпочитал стихотворения с числом строк 8, 131, 211 как более рациональные для выражения мыслей и эмоций.

Обратимся вновь к произведениям А.С.Пушкина. Разглядим композицию «Пиковой дамы». В данной повести кульминационным моментом является сцена в спальне графини, куда просочился Германн в надежде выяснить тайну 3-х карт, сцена, которая оканчивается гибелью графини в повести 853 строчки. Кульминационный момент повести – это погибель графини. Ему отвечает 535 –я строчка. Эта строчка размещена в повести практически буквально в месте золотого сечения, т.к. 853:535=1,6 .

Повесть «Пиковая дама» состоит из 6 глав. Поглядим, не проявляется ли в композиции глав золотая пропорция? В первой главе золотому сечению отвечает 68 строка (всего в главе 110 строк). Но ведь это узловая точка повествования, в ней переломный момент всей главы: откроет ли Сен — Жермен свою тайну графине!

2-ая глава повести содержит 219 строк. Золотое сечение тут приходится на 135 строчку. Но ведь это кульминационный момент главы, Лиза увидела в окне стоящего на улице Германна! Отсюда начался для нее новейший отсчет времени, начались действия, определившие всю ее последующую судьбу. А.С.Пушкин совсем буквально обусловил это пространство во 2-ой главе: ведь 219:135 = 1,62.

3-я глава повести обрисовывает усилия Германна попасть в дом старенькой графини, выведать у нее тайну 3-х карт. Это пространство начинает новейший отсчет времени для Германна. Эта ситуация приходится на 131 строчку третьей главы, а всего в ней 212 строк. Разделив 212 на 131, мы получим буквально золотую пропорцию 1,618!

В четвертой главе размером 113 строк золотая пропорция приходится на 70 строчку. Это также переломный, катастрофический момент в жизни Лизы.

В пятой главе описано посещение Германна похорон графини. 46 строчка пятой главы поделила повествование на две части: 1-ая — похороны графини и 2-ая – сон Германна. Эта 46 строчка также отвечает золотой пропорции, ведь всего в данной главе 75 строк (75:46=1,63).

В крайней главе повести золотая пропорция приходится на 77 строку, которая завершает описание первого денька игры Германна в карты и первого его выигрыша. Как лицезреем, и в композиции крайней главы повести находится золотая пропорция.

Золотая пропорция находится и в композиции остальных произведений Пушкина. В рассказе «Станционный смотритель» 377 строк. Кульминационный момент рассказа – это весть о том, что дочь смотрителя уехала с гусаром. Этот момент отражен во фразе, которая является 214 строчкой. тут практически четкое соответствие золотой пропорции.

В небольшом рассказе «Гробовщик» всего 229 строк. Со 139 строчки начинается описание ужасного сна гробовщика. И тут переломный момент рассказа приходится практически буквально на золотую пропорцию (229:1,618=141 строчка).

Совпадение кульминационных моментов в произведениях А.С.Пушкина с золотой пропорцией умопомрачительно близкое, в границах 1-3 строк. Чувство гармонии у него было развито необычно, что беспристрастно подтверждает Заключение.

Оптимальные и иррациональные числа являются типичными противоположностями. Но природа едина, и ее противоположности не только лишь находятся в противодействии, борьбе, да и в единстве. И не умопомрачительно, что почти все иррациональные числа выражаются через совокупа целых чисел. Все три числа:p, e и Ф – соединены меж собой ординарными отношениями и могут быть выражены в виде пределов нескончаемых дробей. Не считая того, на примере золотой пропорции показано, что целые числа натурального ряда : 1, 2, 3, … могут быть выражены через иррациональное число Ф. Не считая того, число Ф с хоть какой степенью точности быть может выражено через отношение целых чисел. Разве эти примеры не свидетельствуют о единстве оптимального и иррационального в природе?!

Мы так нередко говорим о единстве и борьбе противоположностей, что это понятие сделалось элементарным, само собой разумеющимся и не требующим исследования. Быть может, потому этот базовый законприроды так не много изучен и углублен и, что типично, практически совсем не математизирован. А меж тем он достоин самого пристального исследования и развития – ведь это один из главных, более общих законов мироздания.

Перечень литературы

Н. Васютинский “Золотая пропорция” –М.,”Юная гвардия”, 1990

А. Азевич “20 уроков гармонии” –М., “Школа-Пресс”, 1998

М. Гарднер “Математические головоломки и утехи” –М., “Мир”, 1971

Д. Пидоу “Геометрия и Искусство” – М., “Мир”, 1989

Энциклопедический словарь молодого математика –М.,1989

журнальчик “Квант”, 1973, № 8

Журнальчик “Математика в школе”, 1994, № 2, № 3

]]>